大学の実験科目で実際に実施している実験です． 説明は，運動方程式が理解できることを前提にしています．制御工学（伝達関数，特性方程式，極）を学習済みだとより良いです．
ですが，実際にやってみて制御工学に興味を持ってもらえるなら，それも嬉しいです．

実験の目的

　移動ロボットの多くはＤＣモータで車輪を回転させて移動します．モータへの入力電圧を変化させると各車輪の回転速度が変化します．各車輪の回転速度の組み合わせに応じて，ロボットの並進・旋回速度，およびロボットの走行軌道が変化します．つまり，入力電圧を上手く制御すれば，ロボットの速度や位置を希望の値にすることが可能になります．この入力電圧の制御にはコンピュータを用いて行うことが多いです．コンピュータに理論や経験にもとづいて設計した制御則をプログラミング言語を用いて組み込むことで，ロボットの運動制御が可能になります．
　本実験では，独立に制御できる２つの車輪がついた移動ロボットの軌道制御を行います．ロボットの特性を調べた後，PID制御，および非線形制御則を用いて目標の軌道に追従させる実験を行います．大学で学ぶ理論と対比させながら，実験，考察を行うことで，PID制御の各要素の特徴，システムの極と応答の関係などを実験で調べて，制御系設計についての理解を深めることを目的とします．

ロボットの運動モデル

　この実験では左右のタイヤが独立に制御できる移動ロボットを対象とする．二輪だけのロボットは転倒してしまうので，通常，二輪の移動ロボットではボディのバランスを取るために補助輪（キャスターなど）をつける．補助輪がない場合は倒立二輪ロボットのように鉛直方向の姿勢安定化制御を同時に行う必要があるので制御は複雑になるが，軌道を制御することはできる．この実験で用いるロボットは補助輪がついているので鉛直方向の姿勢制御は考えない．
　まず，ロボットのタイヤは地面に対して滑らないと仮定する．この仮定は自動車が凍った路面でスリップする場合や，急発進や急ブレーキをかけたときにタイヤが空転している場合などでは満たされない．しかし，建物の廊下などを比較的ゆっくり走るロボットでは満たされると考えることができる．つまり，ゆっくり走行するロボットの制御を考える問題においては，この仮定は「妥当」だと言える．
　この仮定の下，ロボットの速度と位置の関係を考えよう．ロボットの位置を表すために，地上に固定した座標系を定義する．この座標系におけるロボットの中心位置（＝左右の車輪の中心位置）を(x, y)とする．また，この座標系のx軸に対するロボットの向き（姿勢角）をθとおく．中心位置(x, y)が変化する速度を並進速度と呼び，これをv₁とする．ロボットが中心位置に対して回転する速度を旋回角速度と呼び，これをv₂とおく（図1）．
　ロボットの並進速度v₁をx軸，y軸方向に分解した成分v_x，v_yは，ロボットの向きθを用いて，それぞれ，
　
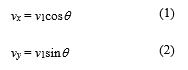
である．位置の時間微分が速度なので，x軸方向の成分についていえば，dx/dt=v_xが成り立つ．したがって，ロボットの位置(x,y)は速度v₁によって，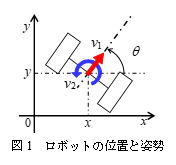
　
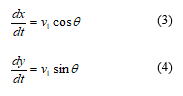
と変化する．一方，姿勢角θは，
　
という式にしたがって変化する．(3)〜(5)式をあわせたものが二輪車両の運動モデルとしてよく用いられる式である．

　このロボットの並進速度と旋回角速度は，左右の車輪速度の組み合わせで制御できる．左右車輪の地面に対する速度をそれぞれv_l，v_rとする．車輪中心の速度v₁は左右車輪速度の平均であるから，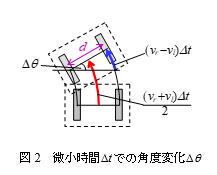　
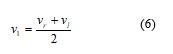
である．左右の車輪速度が異なるとロボットは直進せずに旋回する．この旋回角速度v₂と左右車輪の速度の関係は図2の幾何学的な関係から，
　
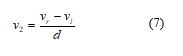
である．

並進速度の制御

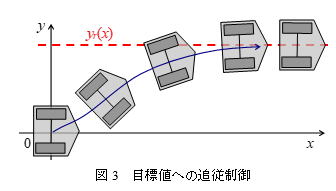
　実験では，ロボットを目標の並進速度v_d (t) で走らせながら，水平面内の関数として与えられた目標軌道y_r (x) に追従させることを考える．y_r(x)が定数の場合は図3のように自動車のレーンチェンジのようなイメージになる．ロボットの状態（位置と速度）を計測し，このロボットの状態を用いてフィードバック制御を行う．
　まず，並進速度を目標のv_d (t) で走らせるための制御について説明する．なお，この制御については後の実験では変更しない．

　並進速度の制御については一定の目標速度での走行を目指すこととし，この目標速度をv_dとする．目標v_dと現在の並進速度v₁(t)の差，つまり偏差（error）を
　
とおく．現在の並進速度が目標のv_dよりも小さい場合，すなわち，e₁(t)>0の場合には加速させて速度を上げ，逆に速すぎれば減速させることで速度を目標に近づける．このような考え方で，並進方向の入力u₁(t)を
　
とする．とする．K_Pは正の定数である．v_dやv₁(t) は速度であり，u₁はモータへの指令値なので次元が異なる．この単位換算の分もK_Pの値を調整することで補う．
　制御則(9)を用いると，目標から大きく離れているときは偏差e₁(t)の絶対値が大きくなって入力u₁(t)の絶対値も大きくなり，逆に目標に近づくと入力は小さくなる．これによって目標軌道に収束することが期待できる．このように，偏差に比例した制御を比例制御とよぶ．しかし，目標に近づいたときに入力を小さくしすぎたせいで定常偏差が残ってしまう場合がある．その場合は過去の偏差の積算値に応じて入力を変化させる積分制御を用いることで改善されることがある．
　
　(10)式のように比例要素と積分要素を組み合わせた制御則をPI制御という．K_P，K_Iは定数であり，それぞれ比例ゲイン，積分ゲインと呼ばれる．これらのゲインの値を調整することでシステムの応答を改善する．