このページは，古典制御の「安定性」について学んだ人向けです．PID制御でロボットの軌道制御を行う際に微分制御が必要であることを線形近似モデルを用いて説明するとともに，線形制御の限界について説明します．
　式はちょっと．．．という方は，とりあえずこのページを飛ばして次の実験に進んでもらって大丈夫です．後で気が向いたら戻ってきてください．

PID制御による軌道制御の理論的な考察

　PID制御では，経験的に知られている各要素の特性にもとづいてゲインを決めることが多いです．例えば，一般に積分要素を入れることで十分時間が経ったときの偏差（定常偏差）の改善が期待できます．また，比例ゲインや微分ゲインを大きくすることで目標値に近づく速さの改善が期待できます．また，制御工学の知識を用いてPIDゲインを決める方法として，限界感度法や，制御対象のモデルにもとづいた極配置法などもあります．こういった知見にもとづいて，PID制御は今も多くのシステムで用いられています．

　しかし，移動ロボットにPID制御を用いた場合，ゲインの組み合わせによってはロボットは全く軌道に追従しなくなってしまうこともあります．
　ここでは，古典制御（線形制御）の考え方と運動モデル(3)～(5)式にもとづいてロボットの軌道制御について解析してみましょう．まず，古典制御の考え方を用いるために，
　　仮定1 ： 並進速度は正の一定値である．
　　仮定2 ： 角度θは十分小さい．
と仮定します．仮定1は一定目標速度v_dに対する追従制御が十分機能している場合，ある程度の時間以降では妥当だと考えてよいでしょう．仮定2は急な旋回をすることなく，直線に沿って移動している場合には満たされると考えることができます．
　仮定1および2が成り立つとすると，(3)式は，
　
となるので，x方向の位置はx(t)=v₁tで変化します．一方，y方向の運動は(4)式の両辺を微分して，(5)式を代入することで，
　
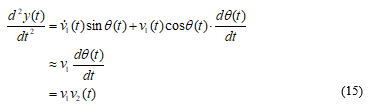
で表わされます．(15)式をラプラス変換すると，v₂からyまでの伝達関数が，
　
と得られます．ここで積分制御を使わないPD制御，すなわち，
　
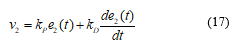
を用いた場合を考えてみましょう．このとき，制御系は図5，

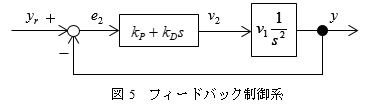
のようなブロック線図で表され，y_rからyまでの伝達関数は，
　
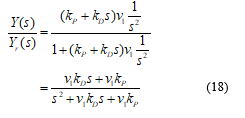
となります．特性多項式がs²+v₁k_Ds+v₁k_Pなので，v₁>0のとき，システムが安定になるための必要十分条件はk_P，k_D > 0です．もし，制御則(17)に微分項を入れない（k_D=0とする）とシステムが安定限界となり，軌道が振動して一定値に収束しないことが予想できます（つまり，このシステムでは微分制御をいれないと目標値に追従しません）．
　また，PD制御(17)を用いれば，十分時間が経ったときに一定値の目標軌道y_rに収束することが期待できます．これは，(18)式に最終値の定理を用いることで確認することができます．
　
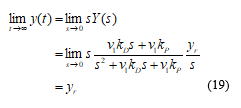
　しかし，実際に実験を行うと偏差が残ってしまうことがあります．この原因の一つとして，前述のモデルではモータの動特性や摩擦などを考えていないことが考えられます．そのため，実験では積分項も加えたPID制御を用いています．

　ところで，実際には並進速度v₁は走り始めた直後は一定値にはなっていません．並進速度が目標値v_dに収束するまでの間や，外乱（例えば床の摩擦の変化）などによってv₁が変動した場合は，仮定1は満たされません．また，旋回入力の制御ゲインを大きくしていくと過渡期でのロボットの角度θが大きくなり，仮定2も満たされなくなります．このように仮定が満たされない状況では，ロボットの運動は(15)式の線形近似モデルには従わなくなり，ロボットが回転してしまうことがあります．(3)～(5)式のような非線形性が強いシステムに対して，線形近似したモデルでの知見にもとづいて制御ゲインを選定することには限界があることに注意してください．

　非線形性を直接考慮した制御則の例として，実験３で用いる制御則があります．実験３で用いる制御則では，変数変換（見方を変える）を用いることで，仮定１，２に関わらず，システムを安定にします．