実験3　非線形制御による軌道追従

　非線形制御則を用いてステップ状の目標軌道yrに追従させましょう．この非線形制御則を用いると，軌道はある線形システムの応答に対応します．そこで，システムの特性方程式の解（極）によって軌道がどう変わるかを調べ，極と応答の関係を考察しましょう．

実験３で使う非線形制御則の説明

　運動モデルの(3)式，(4)式より，
　
である．この式の両辺をxで微分し，(3)式，(5)式を代入すると，
　
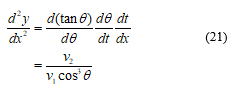
である．ここで，新しい変数uを用いて，
　
とおく．この(22)式を(21)式に代入すると，
　
となる．(23)式はuとyの関係を表す線形モデルである．ただし，時間tのかわりにxに対する変化を表している．このシステムにおいて，位置yを制御するために，PD制御を用いて，
　
としよう（ここは線形制御の考え方です！）．k₀，k₁ > 0は制御ゲインである．
　(24)式の制御ゲインは実験2と同様に決めることができるが，ここではシステムのモデル(23)にもとづいて決める方法の一つを示す．(24)式を(23)式に代入すると，
　
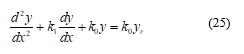
となる．xを時間tの代わりとみなして，両辺をラプラス変換すると，x-y平面内の軌道y(x)の目標関数y_rへの収束はつぎの特性方程式，
　
に支配されることがわかる．この特性方程式の極は，k₀，k₁によって任意の値にできる．極と応答の関係に関して知られている結果から，軌道を速く目標に収束させたければ，特性方程式の解，つまり極が－∞に近づくようにゲインを決めればよい．また，過渡状態での振動を抑えたければ実数極になるようにゲインを決めればよい．
　例えば，極をp₁，p₂にしたいときは，(26)式と(s－p₁) (s－p₂ ) = 0，すなわち， 　
　
が等しくなるようにk₀，k₁を決めればよい．このような方法を極配置法（pole placement method，またはpole assignment method）という．この方法は制御対象のモデルにもとづいて理論的に制御則を求めるものである．このような方法を用いるためには理論的な知識を必要とする．しかし，ゲインと応答の関係が理論的に推測できるので，ゲイン調整における試行錯誤が少なくて済む．
　なお，実際の旋回速度入力v₂は，(20)式，(24)式を(22)式に代入した
　
であり，非線形関数を用いた状態フィードバック制御となる．

実験手順

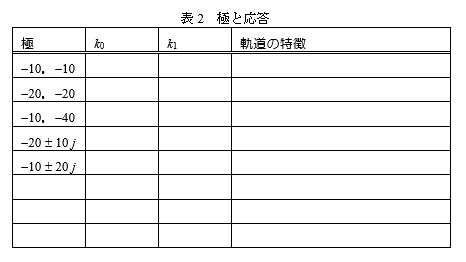
　実験の前に， 制御されたロボットの軌道を支配する特性方程式，s²+k₁s+k₀=0 (26) の極が以下の値になるように，ゲインk₀とk₁を計算してください．

　 0.　PCとロボットをつなぎます．（PCの右側のUSBポートに接続）　

1. VCforRobodesignerCOM＊.exeを実行します．
2. PC画面で「非線形制御」を選びます．
3. Control gainsの数字を入力します．
   　　例：k0 = 400　k1 = 40
4. 目標速度を入力します（単位はmm/s，デフォルト値は100mm/sです）．
   　　例：vd = 100　mm/s　
5. 目標軌道を入力します．
   　　例：y(x) = 100　mm
6. 停止させるx軸方向の位置を入力します（単位はmm，デフォルト値は500mmです．走行できる場所があれば長くしても構いません）．
   　　例：xが　500　mmに到達したら停止します．
7. 「パラメータ送信」ボタンをクリックします．メッセージにしたがって，ロボットの周囲を片付けたら，メッセージウィンドウを閉じます．エラーメッセージが出た場合は，10へ飛んでプログラムを終了し，1からやり直しです．
8. ロボットの基板の真ん中付近にあるpushボタンを押します（図9 Ⓐ）．0.5秒後にロボットが動き出します．
9. PC画面のグラフをWindowsのSnipping ToolやPaintなどを用いて保存してください．数値データについても実験１と同様に保存されています．
10. PCのソフトウェアを終了します．
11. ロボットのリセットボタンを押します（図9 Ⓑ）←忘れずに！
12. 表2のk0，k1を用いて，1)から11)の手順を繰り返して，走行軌道を比較します．
13. 12の結果にもとづいて，オーバーシュートがなく，できるだけ速く目標軌道に追従するようなゲインの組み合わせを探し，そのときの極の値を計算しましょう．
14. 13のゲインを用いて，目標速度を50mm/s，150mm/sに変更して，100mm/sのときと軌道を比較しましょう．
    

結果と考察

• 結果３
  ・k0，k1を変更して実験を行い，応答を比較して表2に特徴をまとめましょう．そのうえで，特性方程式の解（極）が実数の場合と複素数の場合，またその絶対値の大きさによって，ロボットの軌道がどうかわるか，特徴をまとめましょう．
  ・目標速度を変更したときの走行軌道を比較しましょう．
• 考察３
  ・極と応答の関係について一般的に知られていること（制御工学の書籍を参照）と実験結果を比較し，どのような場合に理論と一致しているか，または一致していないかをまとめたうえで，その理由を考察しましょう．