時間微分と位置、速度、加速度との関係
位置をベクトル r とし直行座標でその成分を次のように表すことにする.
In[1]:=
![]()
Out[1]=
![]()
速度 v はr を時間tで微分すればよい.
In[2]:=
![]()
Out[2]=
![]()
これはMathematicaの表記方法で不慣れと思われるが通常の表記だと
In[3]:=
![]()
Out[3]=
![]()
と書ける.(メニューでCell , Convert To,TraditionalFormと選べばよい.)
加速度 a は
In[4]:=
![]()
Out[4]=
![]()
または、
In[5]:=
![]()
Out[5]=
![]()
と書ける.
等加速度運動
等加速度運動とは加速度 a がコンスタント(一定、時間によらない)である運動をいう.
In[6]:=
![]()
ここで上で定義したa, v の定義を消しておいた.
速度を求める.
In[7]:=
![]()
Out[7]=
![]()
Mathematica では不定積分の積分常数は表記されない.
t = 0 のときv = v0であったとすると、
In[8]:=
![]()
Out[8]=
![]()
位置を求める.
In[9]:=
![]()
Out[9]=
![]()
t = 0 のときr = r0であったとすると、
In[10]:=
![]()
Out[10]=
![]()
となる.
たとえば v, r 間の関係は、
In[11]:=
![]()
In[12]:=
![]()
Out[12]=
![]()
または、
![]()
となり、よく知られた関係を得る.
練習問題
例題:重力場で質量m の物体が水平面に対し角度θ の方向に速さvで投げられた場合の運動を論ぜよ.
水平方向の座標をx 、垂直方向の座標をy とする.ニュートンの第二法則をもちいると
In[13]:=
![]()
Out[13]=
![]()
したがって、x[t]とy[t]との関係式は
In[14]:=
![]()
Out[14]=
![]()
In[15]:=
![]()
Out[15]=
![]()
となり、放物線を描くことになる.
In[16]:=
![]()
Out[16]=
![]()
とも書ける.
これをプロットしてみよう.まず、角度θを45度とし速度vを変える.
In[17]:=
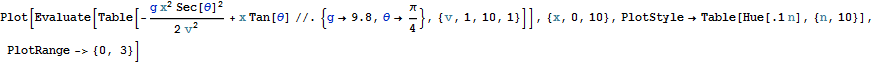
Out[17]=
In[18]:=
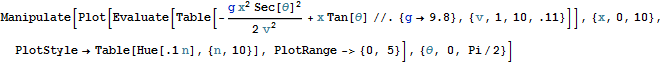
Out[18]=
問1:一般に飛距離xは速度vの関数としてどのように表されるか.
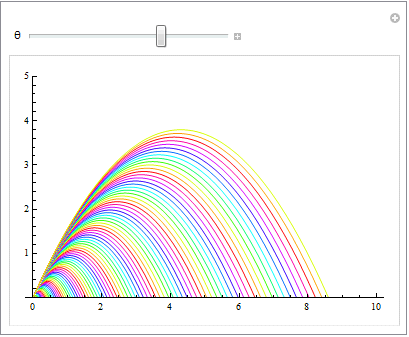
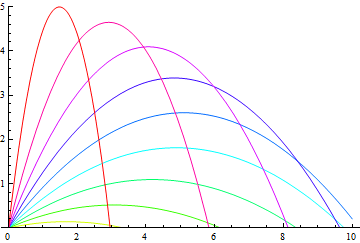
次に速度vを固定し角度θを変える
In[19]:=
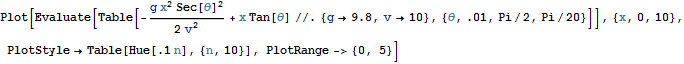
Out[19]=
In[20]:=
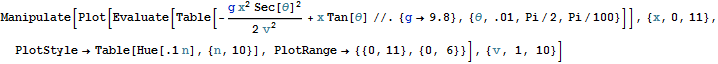
Out[20]=
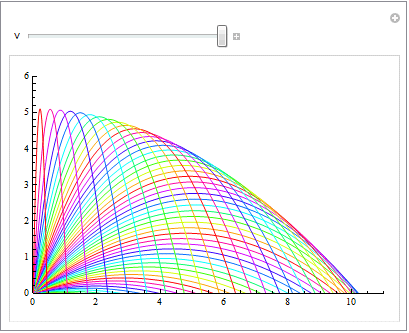
問2:一般に飛距離xが最大値をとる角度θは何か。 また、最大初速度v0が与えられているとき、物体が決して到達できない領域を示せ。
一般的な加速度運動加速度運動
加速度 a が時間t の運動を考えよう.
In[30]:=
![]()
ここで上で定義したa, v の定義を消しておいた.
速度を求める.
In[31]:=
![]()
Out[31]=
![]()
a[t]と加速度がtの関数であると宣言したので、アウトプットが上のようになった.たとえば、
In[32]:=
![]()
Out[32]=
![]()
であったとすると、
In[33]:=
![]()
Out[33]=
![]()
となり、位置xは
In[34]:=
![]()
Out[34]=
![]()
となる.
問3上で求めた位置vは実は正しくない.その理由を考えよ.
問4位置 x が次のように与えられている.速度、加速度を求めよ.
![]()