以下は下付けのシンボルを使うための準備である.
In[1]:=
![]()
In[2]:=
![]()
In[3]:=
![]()
In[4]:=
![]()
Vectors
力、速度、加速度などはベクトル量であり、大きさと方向を持つ.質量は大きさのみでスカラー量である.力学では、ベクトルの加法、減法、内積、外積という演算が重要な意味を持つ.ここでは、簡単にその基本的な性質を述べる.
ベクトルの和
a, bのベクトルを次のようにおく.
In[5]:=
![]()
和は
In[7]:=
![]()
Out[7]=
![]()
となり、各成分を各々たしあわせれば良い.a とb の差は
In[8]:=
![]()
Out[8]=
![]()
となる.
交換則、結合則が成り立つ.すなわち、
In[9]:=
![]()
Out[9]=
![]()
In[10]:=
![]()
Out[10]=
![]()
内積(スカラー積)
内積 (cross product とか dot product) というのはベクトルとベクトルからスカラーをつくる演算を意味し、次のように定義される.
すなわち、a, bのベクトルを次のように
In[11]:=
![]()
と直角座標で表すとするとベクトルa と b の内積は
In[13]:=
![]()
Out[13]=
![]()
と書け、またベクトルa と bの間の角をthetaとすると
In[14]:=
![]()
Out[14]=
![]()
または、
a.b == | a | | b | Cos[θ]
が成り立つ.
例 ベクトルa, b が次のように与えられているときその間の角度を求めよ.
In[15]:=
![]()
解)
In[17]:=
![]()
Out[17]=
![]()
であるから、
In[18]:=
![]()
![]()
Out[18]=
![]()
または、数値では、
In[19]:=
![]()
Out[19]=
![]()
となる.これはラジアンで表されている.もし度に変えたければ
In[20]:=
![]()
![]()
Out[20]=
![]()
問1 ベクトルa, b が次のように与えられているときその間の角度を求めよ.
In[21]:=
![]()
外積
外積 (Cross Product) というのはベクトルとベクトルから新しいベクトルをつくる演算を意味し、次のように定義される.
a, bのベクトルを次のように直角座標で表すとすると
In[23]:=
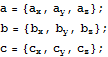
In[26]:=
![]()
Out[26]=
![]()
または、一般の表記法をもちいると
In[27]:=
![]()
Out[27]=
![]()
となる.次の公式が成り立つ.
In[28]:=
![]()
Out[28]=
![]()
In[29]:=
![]()
Out[29]=
![]()
または、
In[30]:=
![]()
Out[30]=
![]()
In[31]:=
![]()
Out[31]=
![]()
問2 Cross[a,a] ==0 であることを示せ.
また、次の公式も成り立つ.
In[32]:=
![]()
Out[32]=
![]()
In[33]:=
![]()
Out[33]=
![]()
すなわち、
In[34]:=
![]()
Out[34]=
![]()
が成り立つ.
特に、ベクトルa, bの間の角度をthetaとすると、
(a×b) == | a | | b | Sin[θ] n
が成り立つ.ここで n はベクトルa, b のどちらにも垂直な単位ベクトルである.(nの方向は右ねじの方向).
例 ベクトルa, b が次のように与えられているときその間の角度を求めよ.
In[35]:=
![]()
解)
In[37]:=
![]()
![]()
Out[37]=
![]()
例 外積を用いて
![]()
であることを示せ.
解)
単位ベクトルa, bを次のように定義する.
In[38]:=
![]()
すると、
In[40]:=
![]()
Out[40]=
![]()
また、単位ベクトルa, b間の角度θは![]() -
-![]() であるから、
であるから、
(a×b) == | a | | b | Sin[θ] n
![]()
が、証明された.
問3 外積を用いて、ベクトルa, b が次のように与えられているときその間の角度を求めよ.
![]()