物理量と単位
物理量には単位がある.力学では、時間(s)、長さ(m)、そして質量 (kg)が単位を構成する基本的な要素である.すなわち、力学(電磁気学を含まない狭い意味の)に表れる全ての単位は上の三つの単位を使えば(組み合わせれば)表される.(電磁気学では上の三つに電荷(C)を付け加えればよい.)
例えば力の単位、ニュートン (N) を考えよう.これは力は(質量かける加速度)と定義されているから(F = m a)
![]()
Mathematica (単位の表記を変換)
Mathematica を用いて単位の表記を変換することができる.まず
In[1]:=
![]()
を実行する.これはMiscellaneousというフォルダにあるUnitsというサブルーティンを呼ぶことを意味する.ここで<<というのは、
In[2]:=
![]()
という、コマンドである.? マークをつけてコマンドを入力すればその説明が出る.ここで、 Convert を使おう.Convert というのは
In[3]:=
![]()

ということを行ってくれるのであるが、残念ながら、まだ日本語化されていない.
In[4]:=
![]()
Out[4]=
![]()
となる.この結果はもちろんあまりおもしろくないが、1NをCGS系(cm, gram, secondを使う)で書くと
In[5]:=
![]()
Out[5]=
![]()
となる.1 m が何フィートかというと
In[6]:=
![]()
Out[6]=
![]()
単位系を変えたいときはSI, MKS, CGSなどを使えばよい.例えばダインをニュートンで表したければ
In[7]:=
![]()
Out[7]=
![]()
In[8]:=
![]()
Out[8]=
![]()
気圧(Atmosphere)をSI系で表すと
In[9]:=
![]()
Out[9]=
![]()
ここでパスカルというのは
In[10]:=
![]()
![]()
である.
問1
(a)三次元物体の密度の単位はSI系で何か.
(b)速度の単位はSI系で何か.
(c)加速度の単位はSI系で何か.
(d)PascalをMKS系で書き換えるとどのように表されるか.
次元解析
物理量には次元という概念が存在する.次元というのは単位系によらない.例えば、長さxの次元は[x] = L, 質量mの次元は[m] =M, 時間tの次元は[t] = Tとかく.加速度aの次元は
In[9]:=
![]()
例
等速円運動を物体が続けるためには向心力(centripetal force) f が必要である.f は物体の質量 m、運動する円の半径 r、その速度 v という物理量だけに依存するはずである.すなわち
![]()
が成り立つ.すなわち
In[11]:=
![]()
Out[11]=
![]()
より
![]()
と向心力 f が表されるということがわかる.(定数は次元解析では出てこない.この場合定数は1である.
問2
(a) 単振り子の周期Tを測定すると、
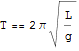
で与えられる.ただし、Lは振り子の長さ、gは重力加速度である.この式は次元的に正しいことを示せ.
(b)ニュートンの万有引力の法則は
![]()
とかける.だだし、Fは重力、M,mは質量、rは物体間の距離を表す.比例定数GのSI系での単位は何か.