の曲線群の微分方程式を求めよう。
第一章 微分方程式
§1 微分方程式と曲線群
問１
の曲線群の微分方程式を求めよう。
In[3]:=
Out[3]=
実際、パラメターｃを変化させて曲線群をプロットしてみる。
In[63]:=
Out[63]=
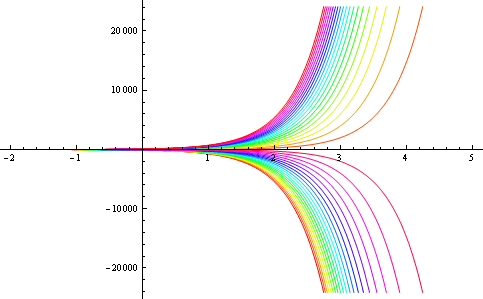
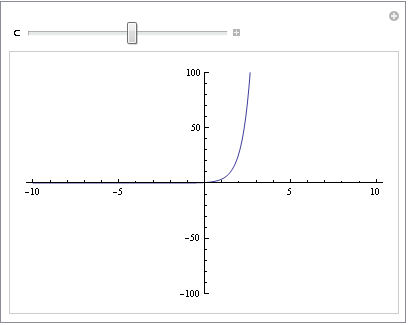
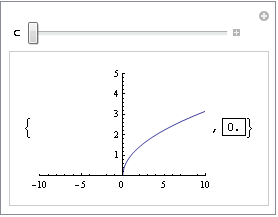
Manipulateを使ってインタラクティブに操作してみよう。
In[68]:=
Out[68]=
次に 
の曲線群を求めてみよう。
In[2]:=
In[3]:=
Out[3]=
アウトプットをTraditional form にすると
Out[3]=
In[11]:=
Out[11]=
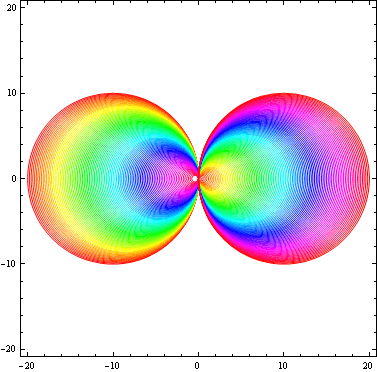
In[16]:=
Out[16]=
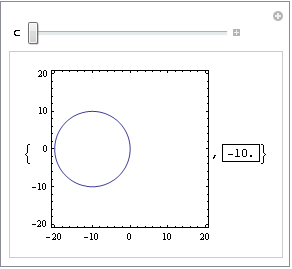
問2
の曲線群を求めてみよう。
In[17]:=
In[18]:=
Out[18]=
または、
Out[18]=
次に y-(b cos(2 x)+a sin(2 x))==0 の曲線群を求めてみよう。
In[19]:=
Out[19]=
または、
Out[19]=
問題
１．（１）
の曲線群を求める。
In[20]:=
Out[20]=
または、
Out[20]=
In[25]:=
Out[25]=
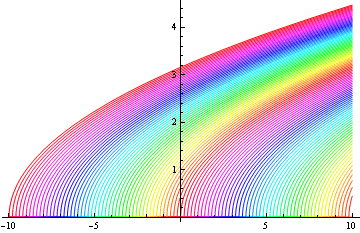
In[31]:=
Out[31]=
１．（２）
の曲線群を求める。
In[32]:=
Out[32]=
または、
Out[32]=
Mathematicaで逆に微分方程式を解いてみよう。以下の解が元の
式と等しいことに注意せよ。(
がｃとなる。）
In[33]:=
Out[33]=
In[38]:=
Out[38]=
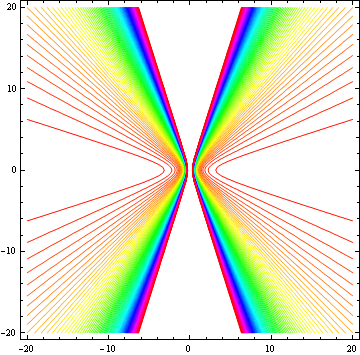
１．（３）
の曲線群を求める。
In[3]:=
Out[3]=
Out[3]=
Mathematicaで逆に微分方程式を解いてみよう。以下の解が元の
式と等しいことに注意せよ。
In[4]:=
Out[4]=
In[5]:=
Out[5]=
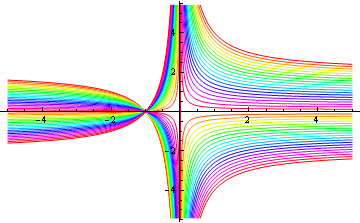
２，（１）
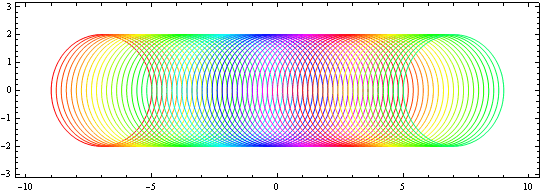
x 軸上に中心を持つ半径２の円の群の微分方程式は
In[6]:=
Out[6]=
または、
Out[6]=
In[15]:=
Out[15]=
２，（２）
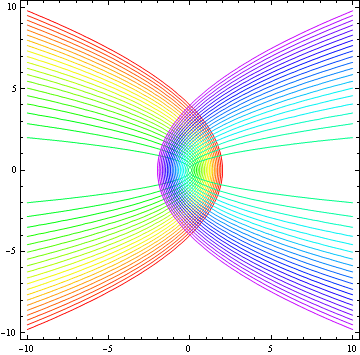
原点を焦点とし、軸がx軸の放物線の群 
In[16]:=
Out[16]=
または、
Out[16]=
In[19]:=
Out[19]=
In[24]:=
Out[24]=
In[25]:=
Out[25]=
２，（３）
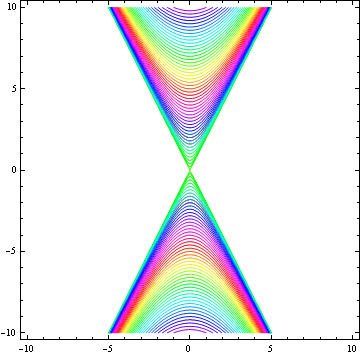
原点が中心、２直線 y=+-2xを漸近線とする双曲線の群
In[20]:=
Out[20]=
または、
Out[20]=
In[32]:=
Out[32]=
§2 微分方程式の解
例題１
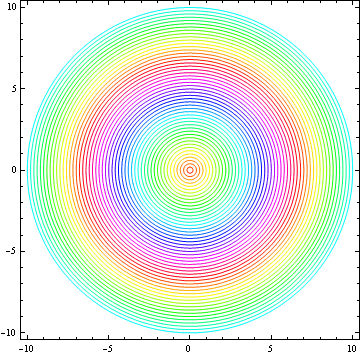
同心円群の微分方程式を解いてみよう。
In[33]:=
Out[33]=
これは
と同等であるから、曲線群を描くと
In[35]:=
Out[35]=
例題２
を解いてみよう。
In[31]:=
Out[31]=
これは y = (x - c)^2 と同等であるので、その曲線群は
In[36]:=
Out[36]=
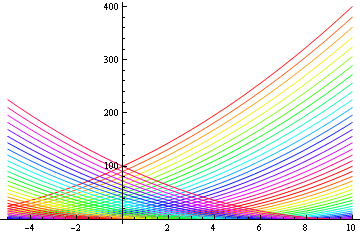
演習問題 １−１ [A]
1 (1)
In[38]:=
In[39]:=
Out[39]=
1 (2)
In[40]:=
Out[40]=
1 (3)
In[41]:=
Out[41]=
または、
Out[41]=
1 (4)
In[42]:=
Out[42]=
Out[42]=
2 (1)
まず、
をプロットする。
In[43]:=
Out[43]=
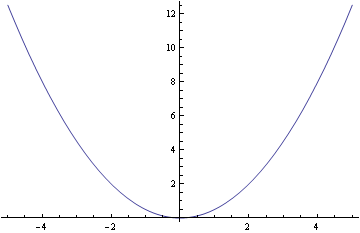
接線は x = c のとき 傾きがｃで ｙは c^2/2 の値を取るので、曲線群は 
.
In[50]:=
Out[50]=
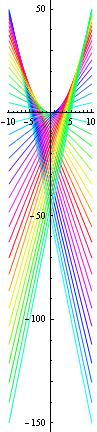
曲線群の微分方程式は以下のように求めることができる。
In[41]:=
In[42]:=
Out[42]=
Out[42]=
