Mathematica とは何か.
以下は,計算の例です.入力セルのどこにカーソルを置いても,[SHIFT]-[ENTER]を押すことができます.
![]()
πを100桁計算しましょう.
![]()
![]()
![]()
ノートブックで微分・積分の計算を行う
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
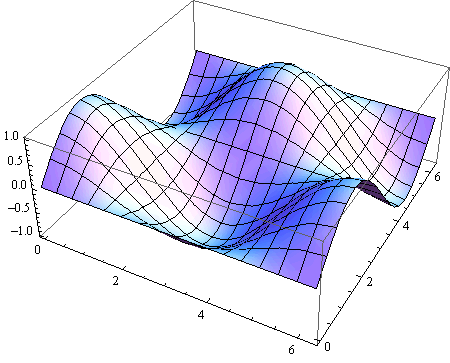
2D,3Dグラフィックスの作成
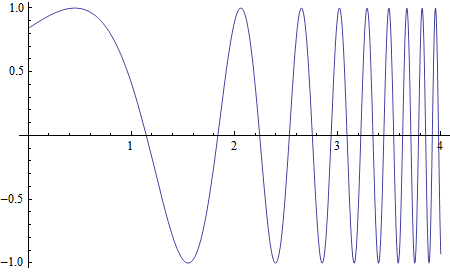
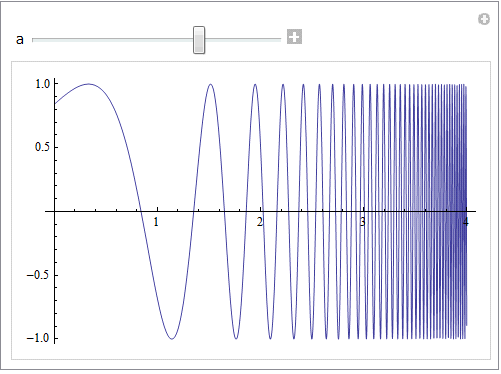
これは1変数の関数のプロットです.リスト{x, 0, 4}がプロットの範囲を指定しています.
In[76]:=
![]()
Out[76]=
In[77]:=
![]()
Out[77]=
In[78]:=
![]()
Out[78]=
In[79]:=
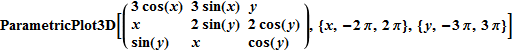
Out[79]=
In[80]:=
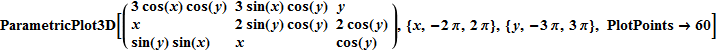
Out[80]=
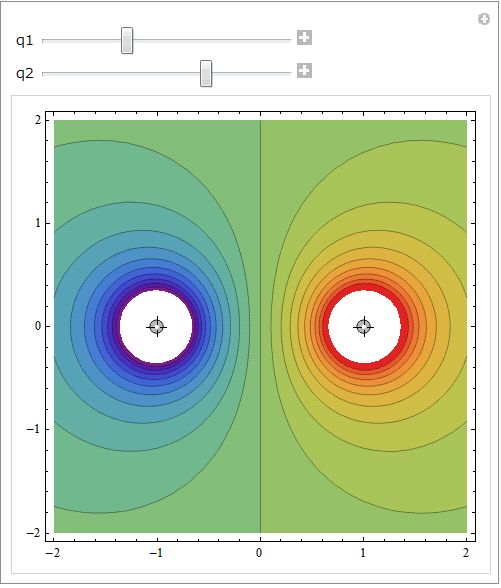
点電荷で生成される静電ポテンシャルを操作する:
In[81]:=

Out[81]=
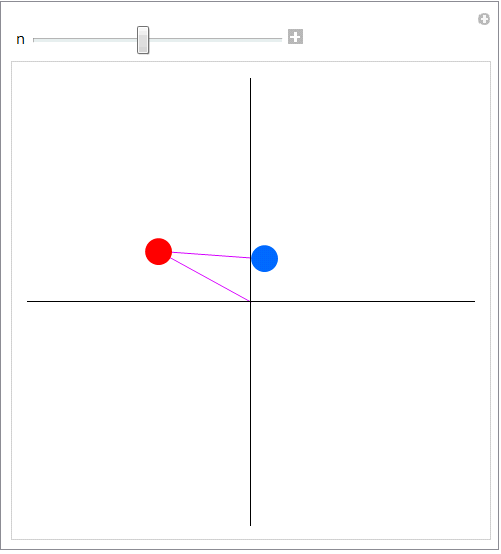
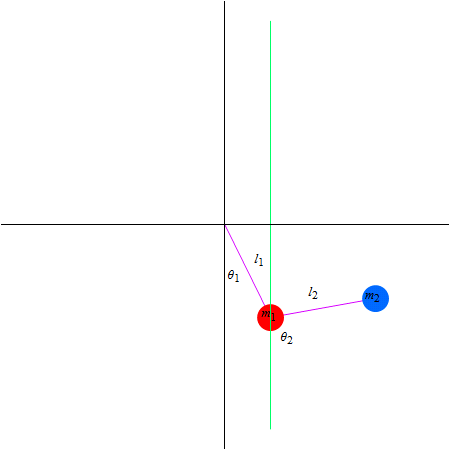
二重振り子
注意:うまくアニメーションが作れないとき
パラメターの値が固定されている場合、うまくアニメーションが作れないときがあります.カーネルを終了して(評価ー>カーネルを終了(Q))もう一度、トライしてください.
はじめに
二重振り子の運動は振幅が十分小さいときには線形な微分方程式で記述できるが、一般には複雑な非線形運動を行う.この系は散逸系ではないカオスを出現できる系として知られている.ここではその運動を記述する微分方程式を導きだし、運動のアニメーションをつくることにする.
次の様な座標とパラメターを下図のように設定する.
In[1]:=

Out[2]=
それぞれの質量の位置を表す座標を次のようにする.
In[3]:=
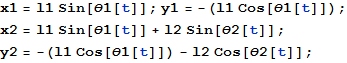
運動は次の微分方程式に従う.(詳細は割愛).
![]()
![]()
実際の計算
ここで数値計算をすることにする.次のようにNDSolveを用いればいろいろなパラメターや初期値に対応する解が得られる.
In[6]:=
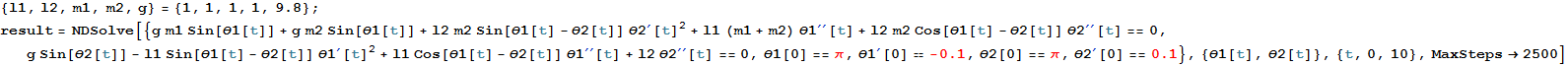
Out[7]=
![]()
In[8]:=
![]()
In[10]:=

In[11]:=
![]()
Out[11]=