この微分方程式を初期条件、t = 0 の時、x =
, v = 
として解いてみよう．
初期条件と単振動の振る舞い
１次元の単振動は次の微分方程式の解を求めればよい．
この微分方程式を初期条件、t = 0 の時、x = , v = として解いてみよ
う．
In[1]:=
Out[1]=
である．この解をx[t] として定義するには、
In[2]:=
Out[2]=
とすればよい．従って、速度 v[t] はこの x[t] を使って次のように求められる．
In[3]:=
Out[3]=
もちろん，約分できるので
In[4]:=
Out[4]=
例えば、
の値を変えつつ位置x[t] を３次元的にプロットしてみよう．
In[5]:=
Out[5]=
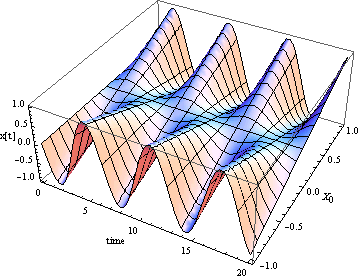
問１ 初期条件、t = 0 の時、x = A cos δ, v = -A ω sin δ として
を解け．x[t] を上で定義してしまったので、その定義を消去するためにClear[x] とイン
プットしておくことに注意．
微分方程式 
の一般解は
x = A cos (ωt + δ)
と書ける． A は振幅 (amplitude) 、δ は位相 (phase angle) と呼ばれ、その値は初期条件
によって決まる．
系の力学的エネルギーをE, 運動エネルギーをK( =
), ポテンシャルエネルギー（位置エネルギー）をU (=
) とすると，
E = K + U ,
すなわち、エネルギー保存則が成り立つ．
問２ 運動方程式
からE = K + Uを導き出せ．k = m 
に注意．
相空間図
ここで相空間の概念について説明し、以下でのカオスについて議論の準備とする．運動の状態を、ただ単に時間の関数 t として記述するのではなく、変位と速度の空間でのイベントとしてとらえるのである．
前述の単振動の場合、運動の状態は完全に時間t の関数として書き表され、二つの量、例えば変位 x(t ) と速度 v (t ) が与えられていれば決まる．x(t ) と v (t ) を二次元空間、即ち平面の座標と考えると、点P (x(t ) , v (t ) ) は振動している粒子の運動状態を記述する．この空間のことを相空間 (phase space) と言う．一般に n 個の自由度のある振動子系だ
と2 n 次元の空間になる．式 
からわかるように、一次元単振動の場合は楕円がその運動に対応する．
単振動の場合の相空間ダイアグラムにおいて軌道は楕円を描く．楕円の大きさはは与えられたエネルギー E に対応する． E の値が大きい程大きな楕円を描く．いかに描く図はあるエネルギーが与えられたときは相空間では粒子の軌跡が楕円であることを踏まて、ParametricPlot[] を使う．複数の軌跡を描くため、Table[] を使い関数の集合をつくり、それをプロットすることにした．位置ｘは 
で与えられることに注意．
In[6]:=
Out[6]=
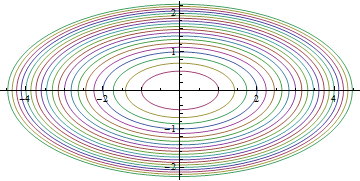
この図には示していないが、相空間の粒子の軌跡は時間の増大に従い、時計周りに回転することに注意する．
問３ 上の入力でもしEvaluateをはずすとどのような答えが得られるか．なぜ，Evaluateが不可欠なのか，説明せよ．
