以下のインプットを実行するには、それをマウスで選び、Shiftを押さえながらReturnを押すか、Enter(キーボードの一番右下)を押して下さい。
単振動
三角関数
まず三角関数の基本的な性質について復習しておこう.
指数関数と三角関数
指数関数と三角関数の間には以下の関係がある(オイラーの公式).
Exp[I x]==Cos[x]+I Sin[x]
![]()
これは、例えば、指数関数、三角関数のTaylor展開をすれば推測できる.即ち、
In[1]:=
![]()
Out[1]=
![]()
In[2]:=
![]()
Out[2]=
![]()
In[3]:=
![]()
Out[3]=
![]()
これらより![]() であることがわかる.Mathematicaで証明するには、
であることがわかる.Mathematicaで証明するには、
In[4]:=
![]()
Out[4]=
![]()
問1 ![]() であることを証明しなさい.
であることを証明しなさい.
加法定理
In[5]:=
![]()
Out[5]=
![]()
すなわち
Sin[α+β]==Cos[β] Sin[α]+Cos[α] Sin[β]
ということを意味する.これが真であるかどうかを調べるには
In[6]:=
![]()
Out[6]=
![]()
となり真実であることがわかる.cosine の場合は、
In[7]:=
![]()
Out[7]=
![]()
すなわち
Cos[α+β]==Cos[α] Cos[β]-Sin[α] Sin[β]
である.
これらを一度に証明するためには上の
![]()
を持ちいる.即ち、
Exp[I(α+β)] ==Cos[α+β]+I Sin[α+β]
であるが、
In[8]:=
![]()
Out[8]=
![]()
より、実部と虚部を比べれば、加法定理が正しいことわかる.
問2 以下の式をTrigExpandを使って展開するとどのような結果がえられるか、実際計算して見なさい.
a) Tan[α+β]
b) Sec[α+β]
c) Csc[α+β]
d) Sin[α+β +γ]
e) Cos[α-2β]
三角関数の複雑な表現を簡単にするためにはSimplify、またはFullSimplifyを使えばよい.例えば
In[9]:=
![]()
Out[9]=
![]()
In[10]:=
![]()
Out[10]=
![]()
問3 以下の式をSimplifyを使って式を簡略化するとどのような結果がえられるか.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
単振動
微分方程式の解
単振動を表す運動方程式は
![]()
と書ける.(上の表現をマウスで選んでセルメニューの形式変換の中の選択を選べばどのように表現がかわるかやってみよう.)ただし、全微分(Dt)を使うとMathematicaは定数まで変数として解釈してしまい問題が起こるので, 偏微分(D)を以後使う.
単振動の解は正弦関数である.これを
In[11]:=
![]()
Out[11]=
![]()
であるとすると
In[12]:=
![]()
Out[12]=
![]()
より
x = A Sin[ω t +δ]
が微分方程式を満足する解であることがわかる.A, δは定数で初期条件によって決まる.
実際に微分方程式を解いてみよう.微分方程式を解くときはDSolveを用いる.
In[13]:=
![]()
Out[13]=
![]()
アウトプットがおかしいのはxが変数ではなく 上で定義した値を持っているからである.x を入力すると
In[14]:=
![]()
Out[14]=
![]()
まず、この値を消しておく.
In[15]:=
![]()
でも良いし、また、
In[16]:=
![]()
でも良い.
x を入力すると
In[17]:=
![]()
Out[17]=
![]()
となり、x に対して何も値が定義されていないことがわかる.もう一度、計算すると
In[18]:=
![]()
Out[18]=
![]()
というアウトプットを得る.これは一般解が二つの定数C[1], C[2]を用いてコサインをサインの和として書き表せることを意味する.
In[19]:=
![]()
Out[19]=
![]()
であるから
C[1] == A Cos[δ]
C[2]==A Sin[δ]
であることがわかる.もちろん、二つの定数C[1], C[2]は初期条件によって決まる.
また、微分方程式
![]()
は
![]()
であるから
![]()
とも書ける.これを積分すると
![]()
となる.ここでEnergy, m は定数である(それぞれエネルギー(運動エネルギーと位置エネルギーの和)、質量に対応している).以下、少し分かりにくいかもしれないが、その計算の手順を示す.
In[20]:=
![]()
Out[20]=
![]()
従って、
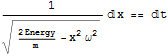
であるから左辺を積分しよう.
In[21]:=
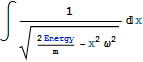
Out[21]=
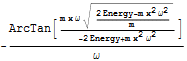
この結果はすこし複雑に見える.FullSimplifyして
In[22]:=
![]()
Out[22]=
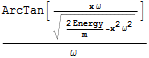
となり、わかりやすい結果を得る.次 x について解いてみよう.ここで積分定数をconstant/ωとする.
In[23]:=
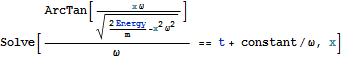
![]()
Out[23]=
![]()
まだ複雑に見えるので、FullSimplifyを使う.
In[24]:=
![]()
Out[24]=
![]()
もう少し簡単にする.
In[25]:=
![]()
Out[25]=
![]()
となり、求めたい結果を得る.変位 x 、速度v は
In[26]:=
![]()
Out[26]=
![]()
In[27]:=
![]()
Out[27]=
![]()
全エネルギーを計算すると
In[28]:=
![]()
Out[28]=
![]()
これを簡単にすると
In[29]:=
![]()
Out[29]=
![]()
となり解が正しいことがわかる.
図を描く.
ここで位置、速度、運動エネルギー、位置エネルギー等を時間の関数としてプロットしてみよう.いま、位置 xは
In[30]:=
![]()
Out[30]=
![]()
であるが、簡単のために
In[31]:=
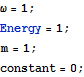
と仮定する.
まず、位置 x を時間の関数としてプロットしてみよう.
In[35]:=
![]()
Out[35]=
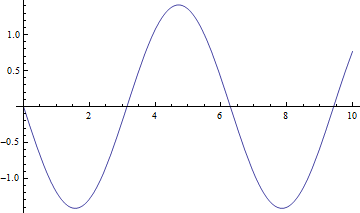
Optionを付けると、
In[36]:=
![]()
Out[36]=
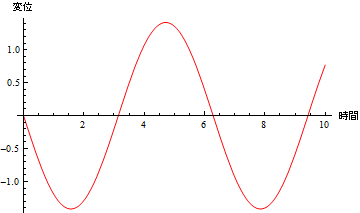
同様に、速度については
In[37]:=
![]()
Out[37]=
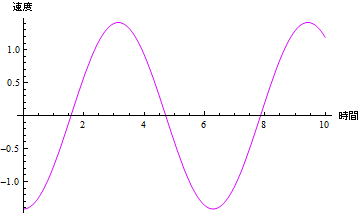
速度は変位に比して位相が90度遅れているのが分かる.加速度は
In[38]:=
![]()
Out[38]=
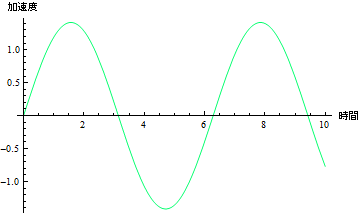
はさらに位相が90度遅れているのが分かる.
さて、運動エネルギーはどうであろうか.
In[39]:=
![]()
Out[39]=
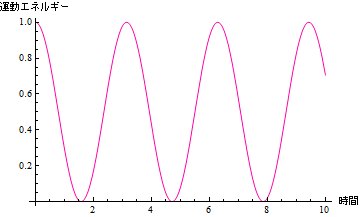
ここでアウトプットのグラフをgraphKineticと呼んだことに注意.位置エネルギーは
In[40]:=
![]()
Out[40]=
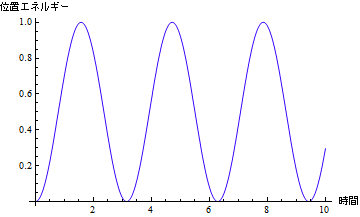
全エネルギーは
In[41]:=
![]()
Out[41]=
以上の図をまとめて描くと、
In[42]:=
![]()
Out[42]=
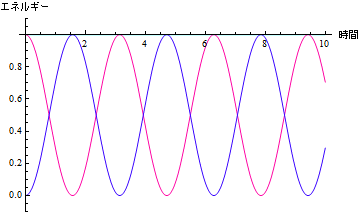
問4 上の図の物理的な解釈を述べよ.(運動エネルギーと位置エネルギー,力学的エネルギーの関係は?)
ここで教科書で説明してある相空間図を描いておく.
In[43]:=
![]()
Out[43]=
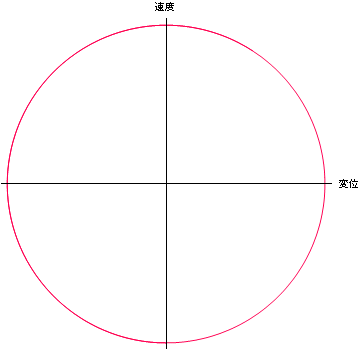
いろいろなエネルギーの相空間図を描きたいときは、
In[44]:=
![]()
In[45]:=
![]()
Out[45]=
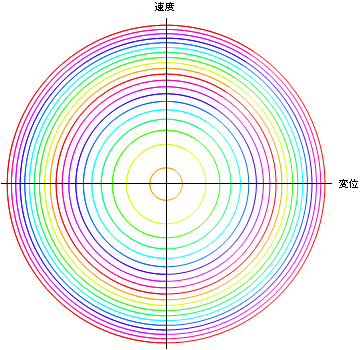
問5 教科書の課題1−1,1−2を解け.
問6 (optional) 教科書の課題1−3,1−4を解け.