Original Mathematica File

強制振動

DSolveを用いてとにかく力任せに解いてみる(brute-force method)

　まず外力が正弦関数的に変化する場合の強制振動の例から論じることにしよう．減衰
振動をする系にこのような外力 F =がかかったとすると、運動方程式は次のように書ける．



または，



ここで， A =/m で，その他の記号の定義はこれまでどうりである．

ここでは力任せに解を求めてみよう．

次の方程式を解く．初期条件はとする．

In[1]:=

Out[1]=

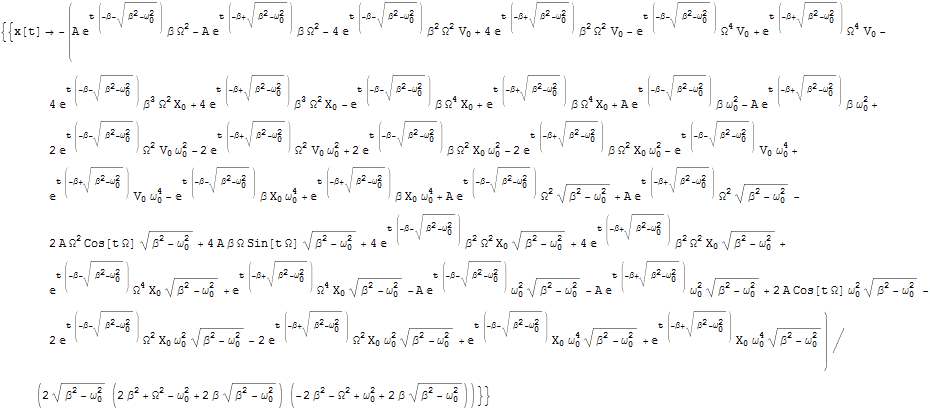
解を定義しておく．その前に，解を少し見やすくしておく．

In[2]:=

Out[2]=

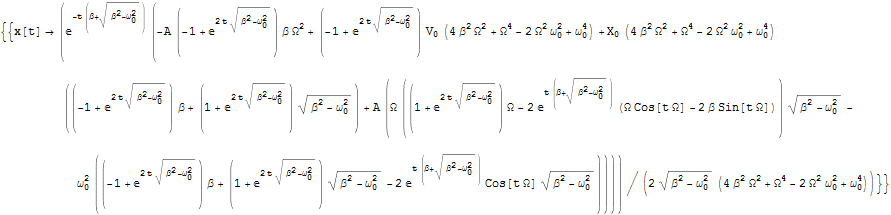
In[3]:=

相当に複雑な解であるが（教科書は振幅、位相等を導入して見やすく書いてある．）、とにかく、変位、速度を適当な初期条件でプロットしてみよう．

変位は

In[4]:=

Out[4]=

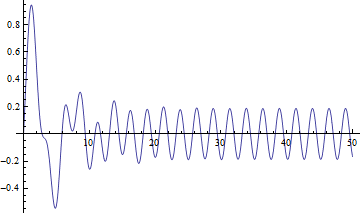
となり、速度は、

In[5]:=

Out[5]=

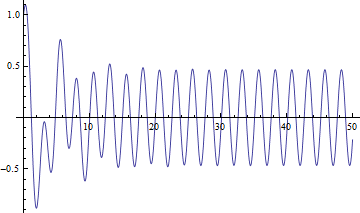
となる．時間tが小さいところは複雑に振動するが、時間がたつと余関数が指数関数的に小さくなり（教科書参照）、特解のみが生き残る．

問１　上の図で時間が十分たったときの角振動数はいくらか．

問２　減衰パラメターbetaをもっと大きくすると系はどのように振る舞うか．

hint:以下のようにベターの値を変えて変位を時間の関数としてプロットしてみなさい．アウトプットはアニメーションで見て下さい．

In[6]:=

Out[6]=

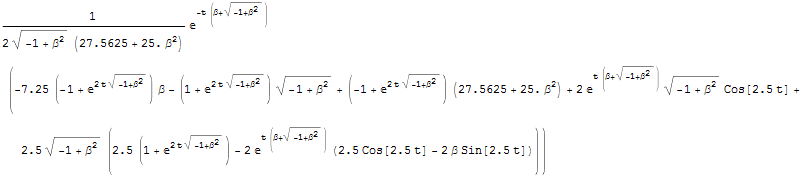
In[7]:=

Out[7]=

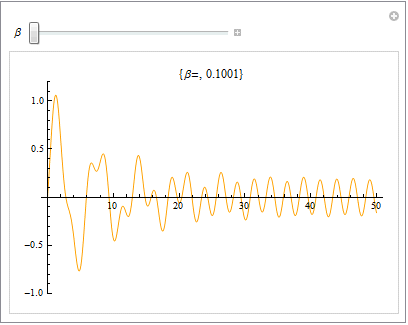
位相空間図

ここでParametricPlotを使って位相空間図を描いてみよう．

In[8]:=

Out[8]=

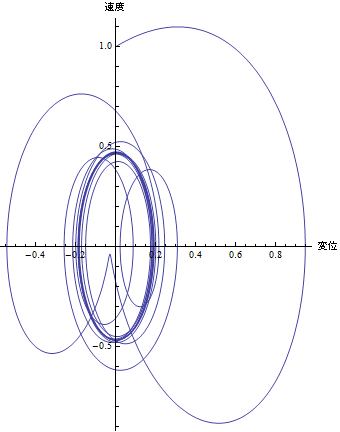
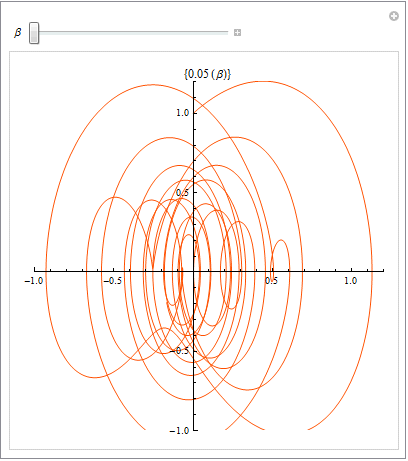
問３　上の位相空間図を解釈せよ．（時間の経過に運動がどのように変わるか．）また、ベターの値を変えると位相空間図はどのように変わるか．

Hint: ベータを変えながら、速度と位置の相空間図を描いてみる．

In[9]:=

In[10]:=

Out[10]=

複素数を用い特解を求める

であることに注意して，

In[11]:=

Out[11]=

と仮定して，与えられた方程式に代入し，B を求める．

In[12]:=

Out[12]=

B を結果のように定義する．

In[13]:=

Out[13]=

B の絶対値 |B| を求めるには、

In[14]:=

Out[14]=

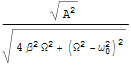
Aが正であるとして，

In[15]:=

Out[15]=

また，偏角をαとすると，αは

In[16]:=

Out[16]=

または，

In[17]:=

Out[17]=

以上より，　の特解はは



で，

Tan[α]=
である．

共鳴

とにかく力任せに解いてみる(brute-force method)の続き

上の結果を使って議論しよう．共鳴とは自然振動数に強制振動の振動数Ωが近づいたとき振幅が大きくなり、位相が大きく変わる現象を言う．（教科書を参照）．

まず、Ωを変えながら位置を時間の関数として３次元的に描いてみよう．

In[18]:=

Out[18]=

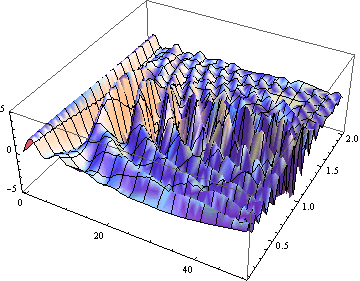
上の図は少しわかりにくのでrotate して真正面から見てみよう．

In[19]:=

Out[19]=

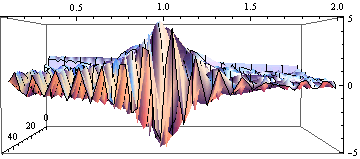
Ω の値が１に近づくと振幅が大きくなる様子が読みとれる．βの値をもう少し小さくすると，

In[20]:=

Out[20]=

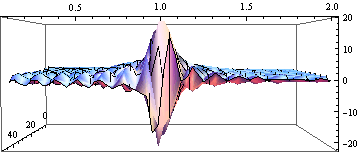
さて、振幅の大きさを見つけよう．時間がたつと系は外力と同じ周期で変化する．時間が十分たったとしてFindMaximumを使って振幅の最大値を探そう．

In[21]:=

Out[21]=

この結果はt =100の近くで最大値を探すと0.187112であるとアウトプットは示している．

OMEGA の値を変えつつ最大値の数列を作ってみよう．（この計算は少し時間がかかる．また，計算が収束しない場合もあるが無視することにする．）

In[22]:=

In[23]:=

Out[23]=

In[24]:=

Out[24]=

Ωがの値（＝１）に近づいたとき振幅が最大値をとると推測できる．

問４　Ωがの値（＝１）に近づいたとき振幅を大きくするためにはどのような減衰パラメターを選べばよいか．

つぎにΩの変化に従いどのように変化するかみよう．

In[25]:=

Out[25]=

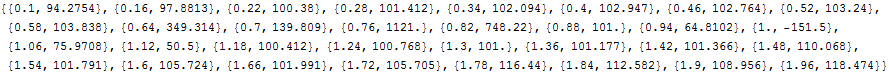
これをプロットすると

In[26]:=

Out[26]=

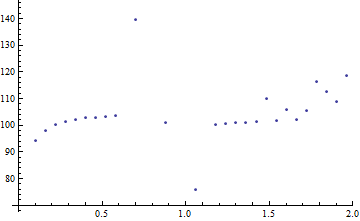
上の図は極小値を与える時間t をOMEGAの関数としてプロットしたものである．従って位相はOMEGAの関数として次のように描ける．

In[27]:=

Out[27]=

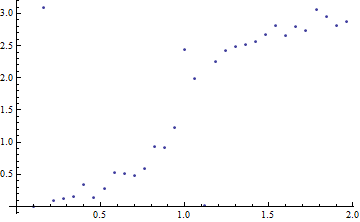
この図は共鳴の起こるところで(OMEGA ~1)で位相が大きく変わる様子が読みとれる．

注：ここで位相が2Piでもとに戻るのでMod を用いた．例としては

In[28]:=

Out[28]=

In[29]:=

Out[29]=

のようにMod[m,n]はmをnで割った残りを示す．

”複素数を用い特解を求める”の続き

興味のあるのは特解のみであるので

In[30]:=

と定義する．

In[31]:=

Out[31]=

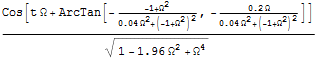
In[32]:=

Out[32]=

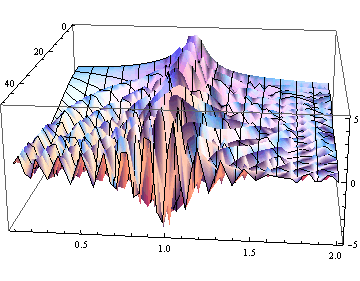
振幅Ｂのみをプロットすると，

In[33]:=

Out[33]=

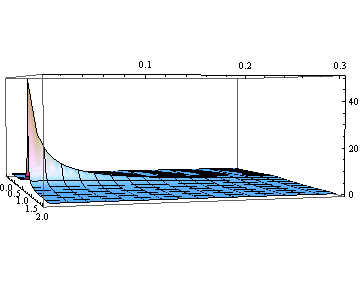
振幅Abs[Ｂ]を最大とする振動数 を振幅共鳴振動数 (amplitude resonancefrequency) という．即ち、

In[34]:=

Out[34]=

より,正の解のみひろうと

In[35]:=

Out[35]=

となる．．これからわかるように β が大きくなれば共鳴振動数 は小さくなり，もっと大きくなると は虚数となり 振幅 は Ω が大きくなるに従い減少する．
β が に比べて小さいとき、共鳴振動数 はほとんど減少しないが、Ω ∼のとき当然振幅 は大きな変化をみせる．

位相のみをプロットすると

In[36]:=

Out[36]=

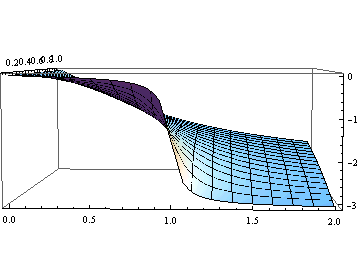
β が小さくなるに従って位相αは自然振動数 の近傍にあるときより急激に変化する．
β = 0 ではその変化が π になることに注意する．

Q値

　強制振動では、よく Q 値というものが引用される．これは共鳴の鋭さをあらわすパラメターで

で定義される． Q 値が大きいほど共鳴は鋭い．ここでは、緩やかな減衰振動の場合、すなわち減衰パラメター β が自然振動数 比べて小さいとき、
Q≈
であることを示す．ここでΔω は半値幅 (FWHM: Full Width at Half Maximum) と呼ばれ、振幅がその最大値の丁度になった２点をむすんだ振動数の幅に対応する．すなわち，

In[37]:=

Out[37]=

を得る．負の解は物理的に意味をなさないので第２番目と第４番目の解のみひろい、 x1と x2 とする．即ち、

In[38]:=

Out[38]=

In[39]:=

Out[39]=

と定義し、半値幅を Δω とよべば、それは、（ b について１次のオーダーのみ計算す
る）

In[40]:=

Out[40]=

In[43]:=

Out[43]=

となる．また，は

In[42]:=

Out[42]=

問５　以上の結果を踏まえ，強制振動とは何か、分かり易く説明せよ．

問６　共鳴とは何か、分かり易く説明せよ．

問７　共強制振動する振動子の力学的エネルギーはどのような時間変化をするか．計算してプロットしてみよ．

Created with Wolfram Mathematica 6