表すことができる.いま,F[t]が周期τ=2π/ωで特徴付けられる周期関数とする.すなわち、任意のt に対して
F[t+τ]=F[t]
とすると、この関数F[t]は次のように展開できる.ここで係数
§4.重ね合わせの原理とフーリエ級数
強制振動においては A cosωt という外力がかかると考えたが、ここでは外力がもう少し複雑な場合を扱う.即ち、減衰振動する系にかかる外力が、ただ単に周期的であると仮定する.この場合は、以下にみるように、この外力をフーリエ級数 (Fourier series) の形にかくことによって、その系の線形微分方程式の解を比較的簡単に求めることができる.しかしながら、これは形式的に解が得られるということであって、実際に解の挙動をみるには Mathematica のようなソフトが不可欠である.
一般に周期的な関数はフーリエ級数で書き
表すことができる.いま,F[t]が周期τ=2π/ωで特徴付けられる周期関数とする.すなわち、任意のt に対して
F[t+τ]=F[t]
とすると、この関数F[t]は次のように展開できる.ここで係数![]() と
と![]() は
は
![]()
ここで
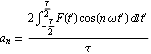
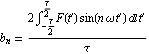
以下の積分に注意
In[1]:=
![]()
Out[1]=
![]()
In[2]:=
![]()
Out[2]=
![]()
In[3]:=
![]()
Out[3]=
![]()
In[4]:=
![]()
Out[4]=
![]()
Mathematica : 鋸歯の形をした周期関数のフーリエ
鋸歯の形をした周期関数をフーリエ級数で表すという問題を考えよう.外力を時間の関数としてプロットしよう.
In[5]:=
![]()
In[6]:=
![]()
Out[6]=
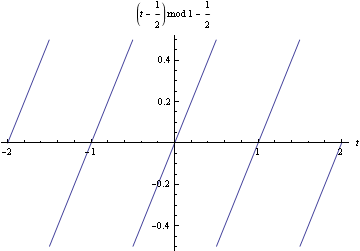
ここでは、Mod[]を使って図をかいた.奇関数であるので常に a[n] =0 である。従って、 b[n] のみ求めればよい。
In[7]:=
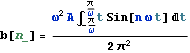
Out[7]=
![]()
nは整数であるので、
In[8]:=
![]()
Out[8]=
![]()
よって
In[9]:=
![]()
例えば、6 項までの展開式をもとめると
In[10]:=
![]()
Out[10]=
![]()
ここで、F(t) を有限項のフーリエ級数で近似した関数 F[t_,ω_,A_, m_] をプロットして
みよう.
In[11]:=
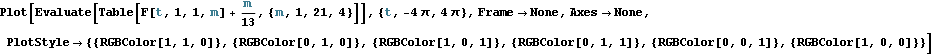
Out[11]=
ここで、Hue[] のかわりに RGBColor[] を使ってカラーを決めた.表現はちょっと長いが、パラメターを三つ使えるので微妙な色変化をコントロールできる.また、図を見やすくするために、各々の曲線を一定量ずらした. Evaluate[] を使わなくても図は描けるが、計算時間が多くかかることになる.関数 F[t_,ω_,A_, m_] が m 大きくなると大変長い式になるからである.
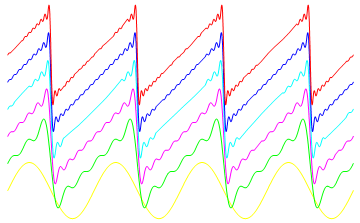
鋸歯形の波形を 400項という有限項のフーリエ級数で近似した関数をプロットしてみよう.
In[12]:=
![]()
Out[12]=
不連続点でオバーシュートすることに注意.PlotPoints を使ったのはオバーシュートが不連続点の近傍のみで起こるため、値を細かくもとめる必要があったためである.400 項までのフーリエ級数であるが、関数の不連続点で値が急に増加しているのがみられる.正弦関数はもちろん連続で微分可能である.もとの鋸型の関数は直線が折れ曲がるところで不連続で微分可能ではない. この不連続点では、一般に項数 m を増やしていくとフーリエ級数の値はもとの関数のその前後の平均値をとり(この場合はゼロ)、その直前と直後ではもとの値より大きくなる.この現象は、1898 年にJ.W. Gibbs が経験的に発見し、ギブス現象 (Gibbs phenomenon) と呼ばれている.これは、無限項の場合でも存在し、正確には、元の値の 8.9490 · · · · %オバーシュートする1.
1. Jerry B. Marion, Stephen T. Thornton, "Classical Dynamics of Particles & Systems", Third Ed., Harcourt Brace Jovanovich, Inc, 1988
不連続点を持つ関数を連続で微分可能な三角関数で近似するということに起因する.
もう少し不連続点の近傍の様子をみるためにその点での拡大図を描いてみよう.
In[13]:=
![]()
Out[13]=
In[14]:=
![]()
Out[14]=
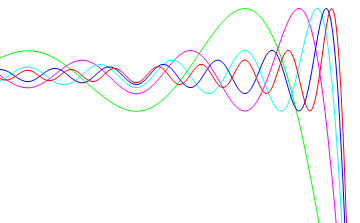
問1上の図からどのような結論が導かれるか。
In[15]:=
FindMaximum[Evaluate[F[t, 1, 1, 1200]], {t, 3.13874}]
Out[15]=
![]()
この結果は振幅が1の 鋸歯波形の場合であるからオバーシュートした分は(0.589073) で%でいえば ~8.9073 %になる.上で述べた値 (8.9490 · · · ·%)よりも少し小さい.勿論、 m の値をもっと 大きくすれ ばこの値に近づく.
問2上に述べた”勿論、 m の値をもっと 大きくすれ ばこの値に近づく”を実際に確かめよ。(真の値に近い値を使わないと、時間がかか
り過ぎたり、間違った値を Mathematica が返してくるので 気をつける必要がある。)下の例は10000項集めた場合を示す。。
In[16]:=
FindMaximum[Evaluate[F[t, 1, 1, 10000]], {t, 3.14128}]
Out[16]=
![]()
高振動数の共鳴のプロット
ここで、外力が具体的に鋸歯波形であたえられている強制振動系の振る舞いをもう少し詳しくみてみることにしよう.系の特解は次のように書ける(教科書参照)。
In[17]:=
K[t_, A_, omega0_, β_, ω_, m_] :=
A*Sum[-((((-1)^n*A)*Cos[n*ω*t - Pi/2 -
ArcTan[(2*β*n*ω)/(omega0^2 -
(n*ω)^2)]])/((n*Pi)*
Sqrt[(omega0^2 - (n*ω)^2)^2 +
4*β^2*(n*ω)^2])), {n, 1, m}]
In[18]:=
![]()
Out[18]=
In[19]:=
![]()
Out[19]=

In[20]:=
![]()
Out[20]=
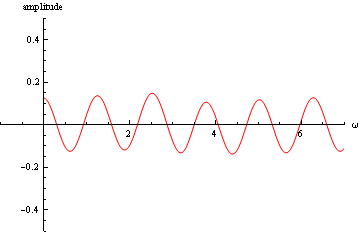
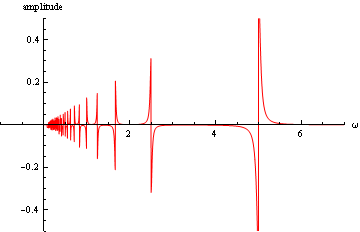
この図は、鋸形の波形であらわされる外力がかかり系が強制振動をする場合、いかに振幅がその外力の角振動数 ω に依存するかを示す. ω = ω0 / n のところで特解 は振幅が大きくなり、位相が急変している様子が読み取れる.n が増えるに従って、相対的な振幅の大きさは減る.
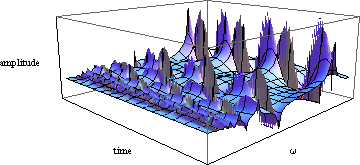
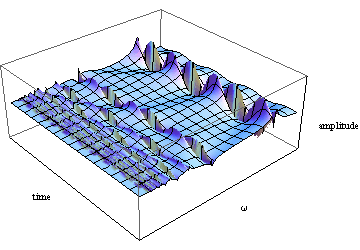
上では時間 t を固定して(ゼロにして)プロットしたが、ここでは、鋸形の波形であらわされる外力がかかり系が強制振動をする場合に、いかに特解 がその外力の角振動数ωと時間 t に依存するかを示す.変数を t とωとして三次元的に描こう.
In[21]:=
![]()
Out[21]=
In[22]:=
![]()
Out[22]=
In[23]:=
![]()
問3次の周期関数のフーリエ級数をもとめよ.![]()
問4 (option) 鋸波形と同様の解析を行い、結果について議論せよ。