減衰振動
教科書に説明してあるように、抗力が速度に比例するとし、その比例定数をk とすると、運動方程式は
と書ける．
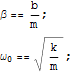
とし、初期条件
として、運動方程式を解いてみよう．
In[1]:=
Out[1]=
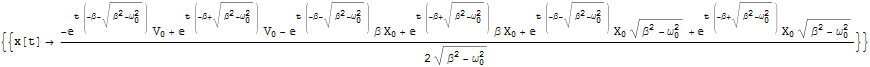
もう少し見やすくしておこう．
In[2]:=
Out[2]=
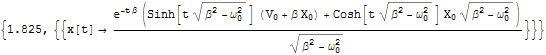
これが上の初期条件を満たす解である． x[t]をこの解であるとすると定義する．
In[3]:=
Out[3]=
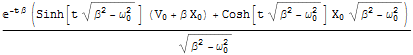
問１ ここで双曲線関数について述べておく．
In[4]:=
Out[4]=
In[5]:=
Out[5]=
In[6]:=
Out[6]=
である．まとめると，、
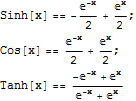
さて、Mathematicaを使わず 以下を証明せよ．
(a) Sinh[i x]==i Sin[x]
(b) 
減衰パラメターがゼロの場合
β =0であるから、
In[7]:=
として、
In[8]:=
Out[8]=
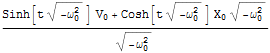
若干見にくいので、
In[9]:=
Out[9]=
としてみると、分かり易い．初期位置を変化させながら、位置を時間の関数としてプロットしてみよう．
In[10]:=
Out[10]=
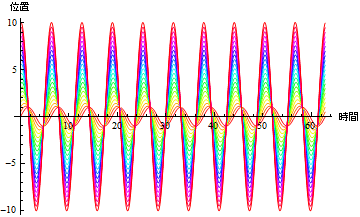
または，
In[11]:=
Out[11]=
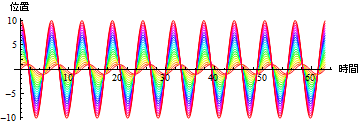
相空間図を描いてみよう．
In[12]:=
Out[12]=
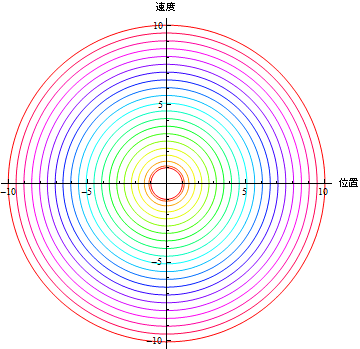
問２ この場合、系の力学的エネルギーはどのような時間変化をするか．実際に運動エネルギーと位置エネルギーの和を計算してみよ．
減衰パラメターが小さい場合(減衰振動)
と仮定する．
β =0と上で定義していたので、
In[13]:=
として．その定義を消しておく．位置は
In[14]:=
Out[14]=
In[15]:=
Out[15]=
である．
減衰パラメターβ を変化させながら、位置を時間の関数としてプロットしてみよう．
In[16]:=
Out[16]=
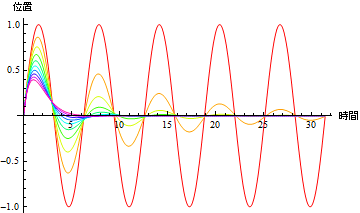
減衰パラメターを変化させながら、相空間図を描いてみよう．
In[17]:=
Out[17]=
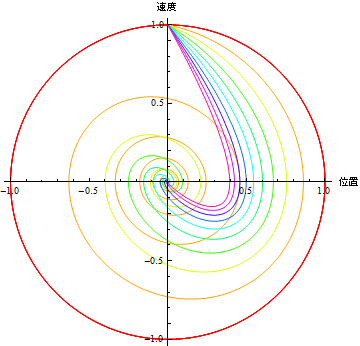
問３ 上の図は何を表しているのか．物理的な解釈を行え．
アニメーション
速度v[t]を以下のように定義しておく．
In[18]:=
Out[18]=
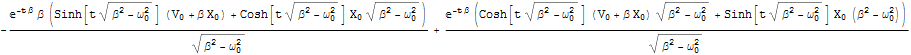
または，
In[19]:=
Out[19]=
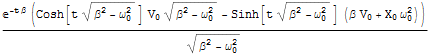
さて、上でつかったgraph1を用いて、減衰パラメターを変化させながら、物体の位置の動きがわかるアニメーションをつくる．
In[20]:=
Out[20]=
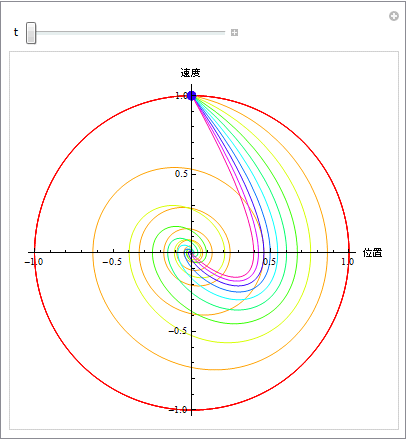
問４ 上のアニメーションから、何がわかるか、物理的に解釈して分かりやすく説明せよ．減衰パラメターβ がゼロに近いとき，また，
に近いときどのように軌跡は振る舞うか．
減衰パラメターが大きい場合(過減衰)
位置は
In[21]:=
Out[21]=
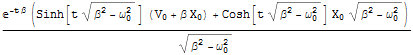
である．
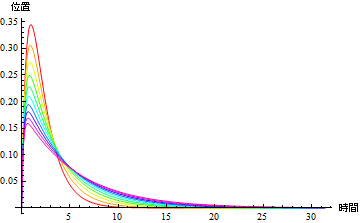
減衰パラメターβ を変化させながら、位置を時間の関数としてプロットしてみよう．
In[22]:=
Out[22]=
減衰パラメターを変化させながら、相空間図を描いてみよう．
In[23]:=
Out[23]=
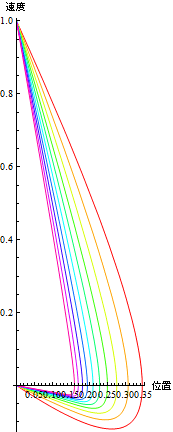
アニメーション
In[24]:=
Out[24]=
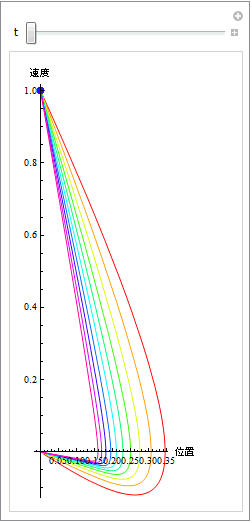
β < 
の時は軌跡は螺旋を描き原点に収束する． β ≥ 
0 の場合は螺旋は描かず直接原点に収束する．この収束した点を 固定点 (fixed point) またはポイントアトラクター (point
attractor) と呼ぶ．このケースでは ポイントアトラクターは一つであるが、カオスを起こしうるの場合では ポイントアトラクター が有数個であったり無い事がある．
問５上のアニメーションを解釈して分かりやすく説明せよ．βの値が何の時一番早く固定点に収束するか．
In[25]:=
Out[25]=
In[26]:=
Out[26]=
減衰パラメターが自然角振動数に等しい場合(臨界減衰)
位置は
In[27]:=
Out[27]=
である．
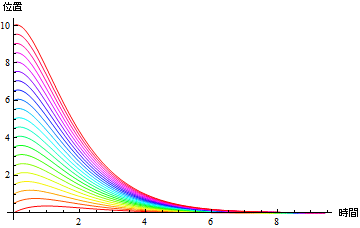
初期位置を変化させながら、位置を時間の関数としてプロットしてみよう．
In[28]:=
Out[28]=
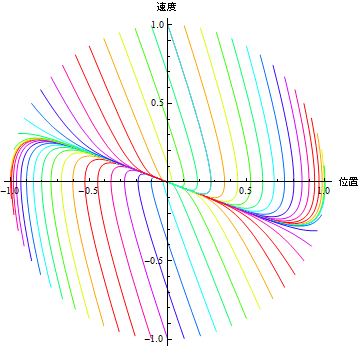
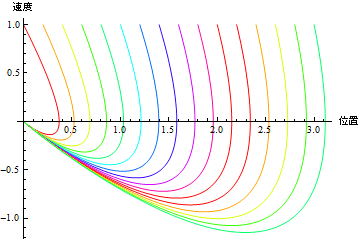
初期位置を変化させながら、相空間図を描いてみよう．
In[29]:=
Out[29]=
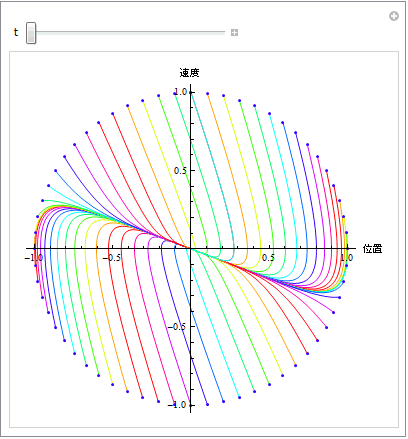
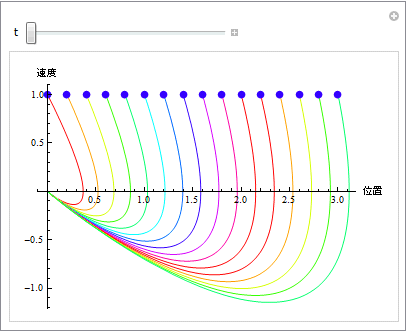
アニメーション
In[30]:=
Out[30]=
In[31]:=
Out[31]=
In[32]:=
Out[32]=
In[33]:=
Out[33]=
In[34]:=
Out[34]=
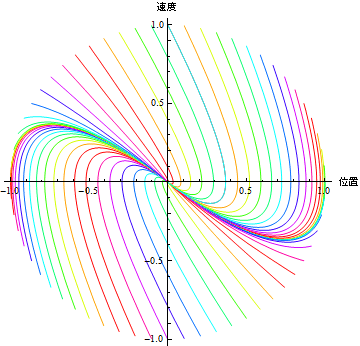
In[35]:=
Out[35]=
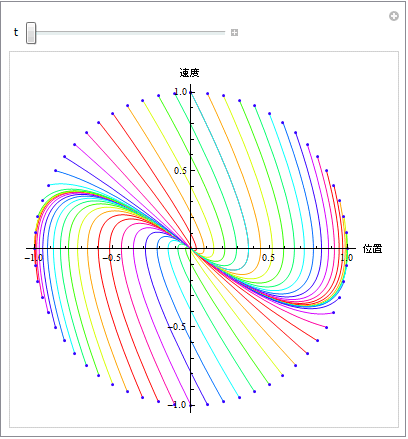
問６上のアニメーションを解釈して臨界減衰について分かりやすく説明せよ．
問７ 過減衰においては、臨界減衰の時に比べて減衰パラメターの値が大きいのに固定点（原点）にたどり着くのに時間が多くかかるのはなぜか．また、どうして時間がたつと、直線に漸近して原点に収束するが、なぜか（教科書を参照）．
問８上のアニメ-ションはわかりやすくするために
の二つのパラメターの大きさの違いによって場合分けをしたが、適当にパラメターを選び、全ての場合を一つの図にして、上と同じようにアニメーションを作るにはどうインプットをすれば良いか．
