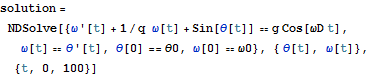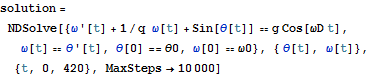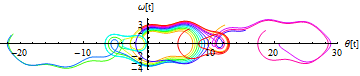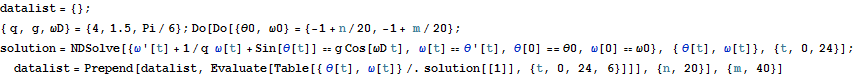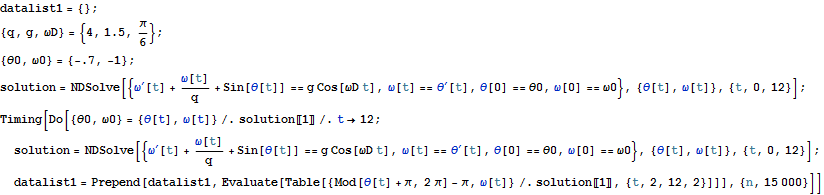カオス
時間変化が非周期的で予想不可能な非線形な系の運動をカオス (Chaos) という．振り子などの機械的に振動する物体、対流する液体、気体、レーザーキャビティー、化学反応などいろいろな系にみられる現象である．カオスの本質は過去におこなった運動を再びおこさないことにある．カオス系の運動を記述する運動方程式ははっきりと未来の運動を予想する (deterministic equations) のであるが、実際の運動は全く規則性を欠き初期条件がほんの少し違うと時間が少したっただけでも全く違う軌道を描く．
わかりやすく説明するために、いまある系がほんの少し違う初期条件で運動を始めたとする．もし、系がカオス的でないとすると、その初期における違いは時間と共に線形に増大する．カオス系はその違いが指数関数的に増大するのである．初期条件がちょと違えばもうその後の運動はあっと言う間に全く違ってしまう．この意味において、カオスでは予想不可能であるといっているのである．このことについて最初に言及したのは HenriPoincare (1854-1912) である．
教科書と同じ方程式を数値的に解くことにする．ただし、全く同じに行ってもおもしろくないので、ここではNDSolve を使って解くことにする．
長さ L の糸の先に質量 m の振り子がぶら下がり、速度に比例する摩擦力
γ m L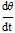 
、それに外力 
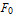cos (
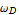t) を受けていると考える．ここで γ は定数で減衰パラメターと呼ぶ．そのときのニュートン の運動方程式は、
m L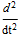 
θ + γ m L
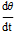+ W sinθ = 
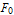cos (
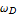t)
とかける．W は重量、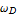 
は外力の角振動数である． ここで、系のパラメターの数を減らすために、振り子の自然振動数 
(= 
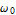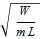) が１であると仮定する．時間はしたがって無単位とみなす．この仮定のもとで、運動方程式は次のようにかきかえられる．
ω'[t] + 1/q ω[t] + Sin[θ[t]] == g Cos[ωD t]
ここで、q はクオリティーパラメター (quality parameter)、 g は外力振幅 (forcing amplitude)と呼ぶことにする． (g を重力の加速度と混同しないように．)
初期条件
正弦関数的な外力が振り子（減衰振動系）にかかっているとする．詳しくは教科書を参照．初期条件を決めて、運動方程式を解こう．例えば、
In[1]:=
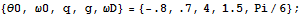
In[2]:=
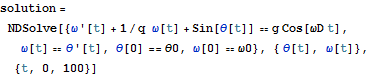
Out[2]=
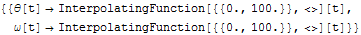
In[3]:=
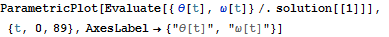
Out[3]=
となり、相空間における軌跡を描くことができる．ここで、相空間での運動の軌跡をさらに長時間にわたって描いてみよう．ただ角度は２Piの周期を持っているので、教科書のように（117ページ)theta の範囲は-PiとPiとの間で描いてみよう．
In[4]:=
Out[4]=
In[5]:=
Out[5]=
これでは、詳細がわかりにくいのでListPlotを使って描き直そう．
In[6]:=
Out[6]=
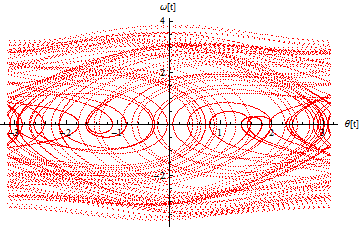
（教科書の口絵15を参照）．
さて、初期値を若干変えて、軌跡がどのように変化するか見るために、いろいろプロットを行ってみよう．
In[10]:=
In[11]:=
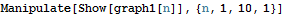
Out[11]=
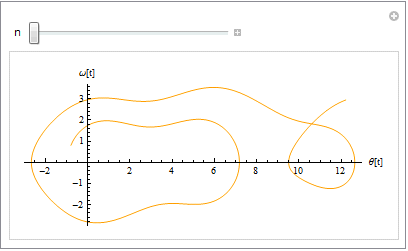
これらのグラフを一つにして描くと、
In[12]:=
Out[12]=
すなわち、初期値が少し違うと運動の軌跡は時間がたつと（上の例では外力の周期の２倍の時間までプロットした．）全く違うものになることが推察できる．
時間が０、半周期、１周期、１．５周期、２周期後の”位置”を描いてみよう．
In[13]:=
In[15]:=
Out[15]=
これらを一つにしてプロットしてみると、
In[16]:=
Out[16]=
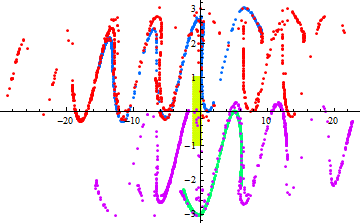
それぞれのデータ点は相空間上に置いて、時間が０、半周期、１周期、１．５周期、２周期後の”位置”を表す点に対応する（上図は教科書の口絵１４に対応する）．初期値が少し違えば大きく拡散することと、ある集合上に（奇妙なアトラクターという）点が集まるであろうことを彷彿させる．
問1
上の例を参考に初期値を
In[14]:=
{ q, g, ωD} = {1., 1., Pi/6};
や
In[15]:=
{ q, g, ωD} = {2, 2.5, Pi/6};
として、同じ計算をし、プロットしてみなさい．結果の考察を行いわかりやすく説明して下さい．（教科書112ページからの記述を参照）．
ポアンカレ断面図
上の例では周期はt=12 である．位相がPi/3, 2Pi/3, Pi, 4/3 Pi, 5/3 Pi, 2Piの時の位相空間での粒子の位置を求めて試しにプロットしてみよう．教科書にもあるようにこれがポアンカレ断面図の例であり、入れ子構造をもつフラクタル図を得ることが出来る．
In[17]:=
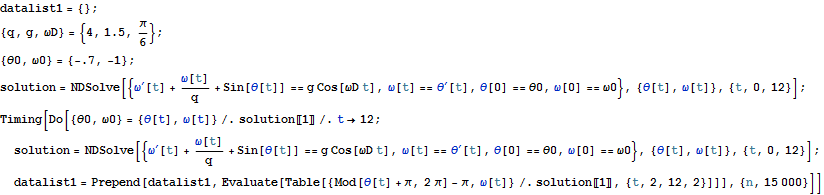
Out[21]=
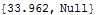
In[23]:=
Out[23]=
In[24]:=
Out[24]=
問２
上の図で位相とポアンカレ図とはどのような関係にあると推測できるか．
問３
上の計算で、時間をもっと長くとってもっとおおくの点をプロットとすると、図はどのように変化するか．
問４
上の計算で、初期値を
In[23]:=
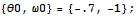
としたが、他の値を使うと結果はどうなるか．
問５
上の計算で、q, g の値を変えて計算をすると結果はどのようになるであろうか．（教科書を参照）．
問 ６
以上、上の考察で得られた結果をもとに、カオスに関する自分の意見をまとめよ。感想でもよい。
