二次元の調和振動子
(教科書:線形・非線形力学とカオスへの入門(7ページから)を参照)
以下、2次元の調和振動子の運動をMathematicaを使って調べてみよう.微分方程式の解き方、初期条件の入力の仕方、リサージュ図形の描き方などを学ぶ.
等方的な場合
![]()
In[1]:=
![]()
Out[1]=
![]()
となり、解が求まる.二階の微分方程式で2次元であるから四つの未知数が表れる.初期条件を時間t=0 の時、
x[0]==A Cos[α], y[0]== BCos[β],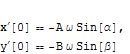
であるとすると、(この初期条件は以下の計算において式が簡単になるように選んだ.このように選んでも一般性が失われないことに注意)
In[2]:=
![]()
Out[2]=
![]()
In[3]:=
![]()
Out[3]=
![]()
In[4]:=
![]()
Out[4]=
![]()
x[t], y[t]を以下のように定義してリサージュ図形を描いてみよう.
In[5]:=
![]()
Out[5]=
![]()
または,
In[6]:=
![]()
Out[6]=
![]()
補足)もちろん上のような面倒なことをしなくても直接DSolveにおいて初期条件を入れてもよい.![]()
まず、A=B=1, α=β=0, ω=1の場合
In[7]:=
![]()
Out[7]=
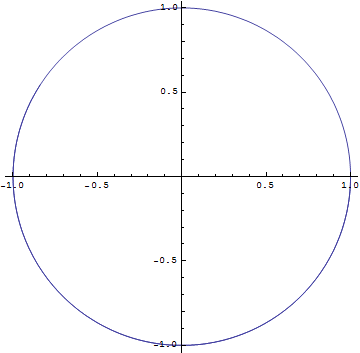
となる.(/.は置き換えを意味する.)
実際、振動子がどのような運動をするのか、アニメーションを作ってみよう.
In[8]:=
![]()
Out[8]=
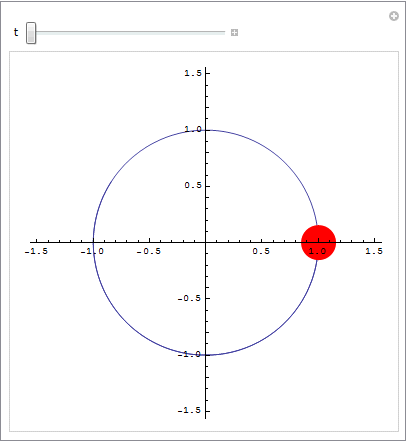
アニメーションのスピードやスッテップ間隔を変えてみよう.
問1以下のMathematica を使って微分方程式を解け.
In[10]:=
![]()
(例) ![]()
In[11]:=
![]()
Out[11]=
![]()
(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)![]()
(6)![]()
問2 以下の質問に実際にMathematica を使ってグラフを描き答えよ.
In[12]:=
![]()
Out[12]=
![]()
とする.
(1) {A→1,B→1,α→0,β→π/2,ω→1} のときどうのようなリサージュ図形がえられるか.
(2) {A→1,B→1,α→0,β→π,ω→1} のときどうのようなリサージュ図形がえられるか.
(3) {A→1,B→1,α→0,β→π/4,ω→1} のときどうのようなリサージュ図形がえられるか.
(4) {A→1,B→1,α→0,β→π/4,ω→1} のときの調和振動子のアニメーションをつくってみよ.(解答用紙にはできたかどうかを書けばよい.)
(5) {A→1,B→1,α→0,β→π/2,ω→1} と {A→1,B→1,α→0,β→3π/2,ω→1} の のときの調和振動子の運動では何が違うか.
非等方的な場合
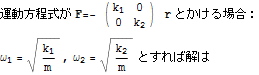
In[13]:=
![]()
Out[13]=
![]()
となる.いろいろなパラメター値にたいするリサージュ図を描いてみよう.
![]()
Out[14]=
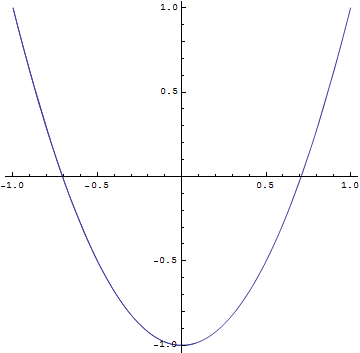
問3 上の図で![]() とするとどのような図形がえられるか.
とするとどのような図形がえられるか.
角振動数の比が無理数の場合は軌跡は閉じない.例えば
![]()
Out[15]=
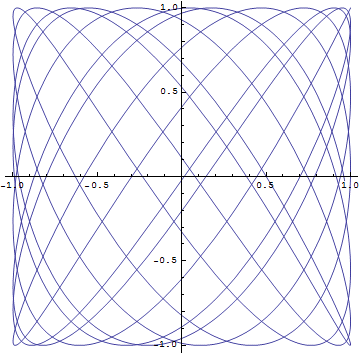
となるが,
問4 上の図で時間tをもっと大きくとるとどのような図が得られるか、結果を解釈せよ.
となるが,
問5 (optional) 教科書、15ページにある図3において、初期角θ=60°で静止していた振り子が描く角度と各速度の相空間図を描け(23ページの図を参照).