
このページを作成した元のMathematica file---Original Mathematica File

二重振り子
はじめに
二重振り子の運動は振幅が十分小さいときには線形な微分方程式で記述できるが、一般には複雑な非線形運動を行う.この系は散逸系ではないカオスを出現できる系として知られている.ここではその運動を記述する微分方程式を導きだし、運動のアニメーションをつくることにする.
![]()
次の様な座標とパラメターを下図のように設定する.

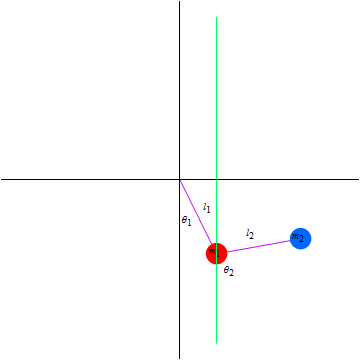
それぞれの質量の位置を表す座標を次のようにする.
![]()
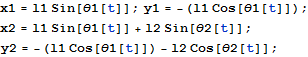
次にラグランジェアン(運動エネルギーと位置エネルギーの差)を求める.
![]()
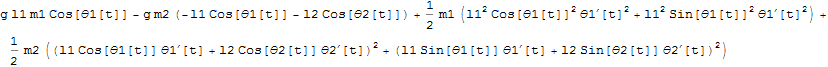
ここで、次のパラメターがコンスタントであることを宣言しておく.
SetAttributes[{l1, l2, m1, m2, g}, Constant]
次の計算でそれぞれの結果(eq1とeq2 )をゼロとおけば、系の運動方程式が得られる.
![]()
![]()
![]()
![]()
運動は次の微分方程式に従う.
![]()
![]()
実際の計算
ここで数値計算をすることにする.次のようにNDSolveを用いればいろいろなパラメターや初期値に対応する解が得られる.
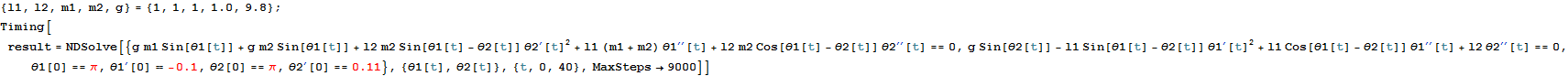
![]()
![]()

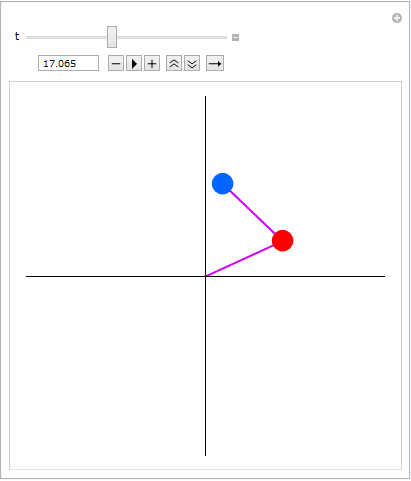
以下は上に挿入したdynamic gifを作成したときの手順.

![]()
![]()