このページを作成した元のMathematica file---Original Mathematica File
二つの重りがバネに繋がれている場合の連成振動

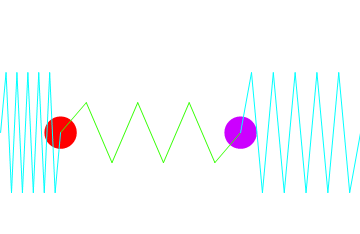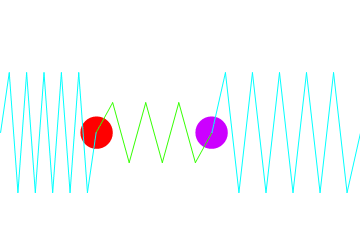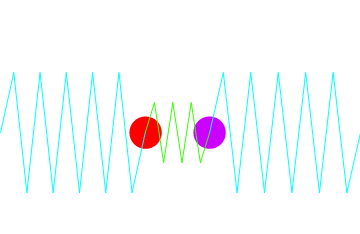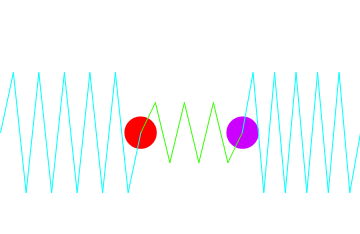
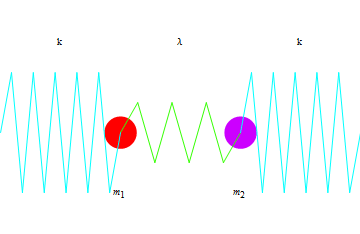
二つ以上の振動子がお互いに作用を及ぼし合いながら振動する場合、これを連成振動という.下図のような場合の運動方程式をとき、振動運動をアニメーションにしてデモンストレートする.
Mathematicaはドローイング用のプログラムではないので次のインプットの例で明らかなように絵を書く場合にはやや面倒である.しかし後にわかるように、すばらしいアニメーションを作り出すことができる.
注意:うまくアニメーションが作れないとき
パラメターの値が固定されている場合、うまくアニメーションが作れないときがあります.パラメーターをリセットしてもう一度、トライしてください.
![]()
パラメター設定

以下のように下付けを定義しておくとSubscript[x, 1]をxの関数と扱わないので便利である.
![]()
![]()
![]()
運動方程式は各々の重りに対してニュートンの第二法則を使って導いてもよいが、ここではLagrangeの方法を使う.
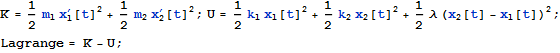
微分方程式はDSolveで解ける
![]()
解くべき微分法方程式は
![]()
![]()
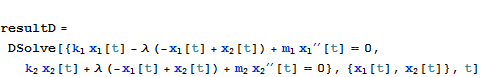

微分方程式は確かにDSolveでも解けるが、解は複雑すぎるので、ここでは数値的に解き、アニメーションを作ることにする.
アニメーションを作ってみよう simulation
ここでは数値的に解くことにする.
![]()
![]()
この計算の結果を横軸を時間に縦軸を振幅として図に描く.

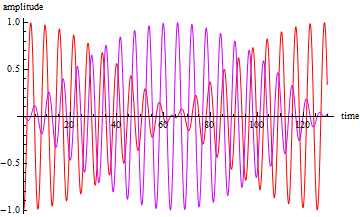
上図より運動のエネルギーが一方の質量から他方に漸次移り、また戻ってくるという様子が窺える.実際、以下をを入力すれば沢山の図がでてきてアニメーションが楽しめる.
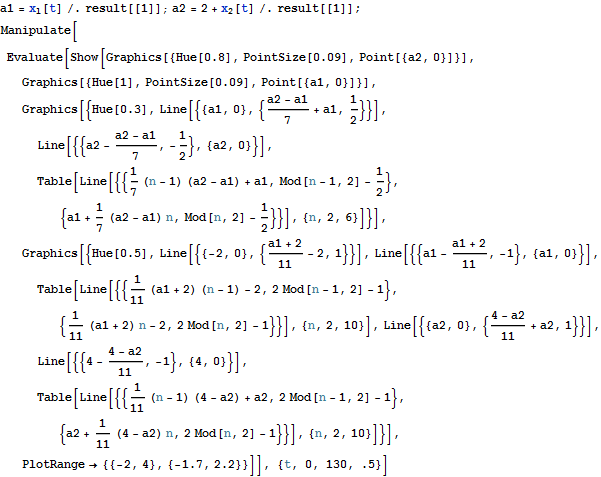
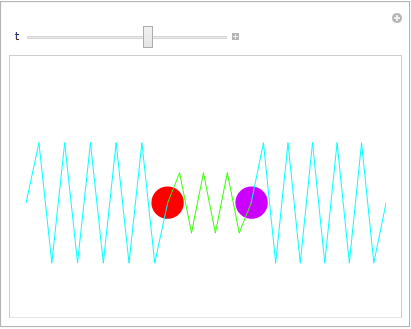
以下は上に挿入したdynamic gifを作成したときの手順.

![]()
![]()