
このページを作成した元のMathematica file---Original Mathematica File
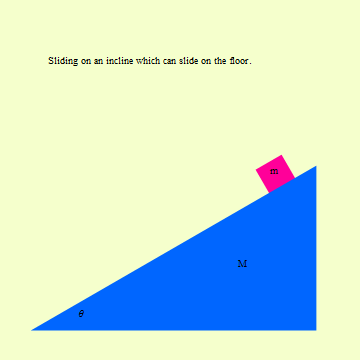
斜面での落下

注意:うまくアニメーションが作れないとき
パラメターの値が固定されている場合、うまくアニメーションが作れないときがあります.パラメーターをリセットしてもう一度、トライしてください.
![]()
台が固定されている場合
例
滑り落ちる距離x[t]は
![]()
であるから、物体の位置{X, Y}は原点をx0滑り落ちたところとすれば、
![]()
![]()
となる.したがって、例えば、


台が滑らかな床に置かれている場合
摩擦のない斜面(水平線とのなす角度をθとする)をもつを質量Mの物体Aと、その斜面を滑り落ちる質量mの物体Bとの運動を考察しよう.物体Bの滑り落ちた距離をx とし、物体Aの重心の水平軸座標をZとする.物体Aと床との摩擦はないものとする.

まず、次の記号の値を消しておく.
![]()
物体Aから物体Bにかかる抗力をR, 物体Bの座標を{X, Y}, 物体Aの座標を{Z, 0}とするとニュートンの第二法則より
![]()
![]()
![]()
の3式が得られる.また、物体Bは物体Aの上に存在するから(constraint condition, 束縛条件)、
( X[t] - Z[t] ) Tan[θ] == Y[t]
でなければならない.運動方程式からRを消去する.
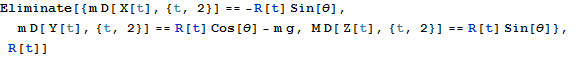
![]()
今度は束縛条件から
![]()
であることに注意してY"を消去する.
![]()
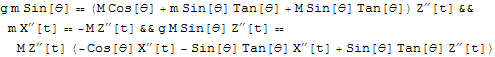
従って、初期条件を次のように仮定して微分方程式を解く.
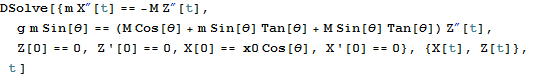
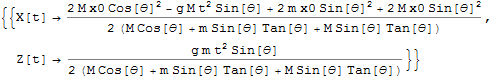
![]()
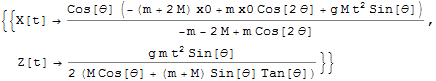
解が求まったのでX, Zの定義を行う.
![]()
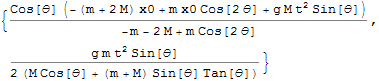
従ってYは
![]()
![]()
となる.運動量を計算すると
![]()
![]()
となり水平方向の線運動量が保存されていることがわかる.エネルギー(運動エネルギーと位置エネルギーの和)はどうか?
![]()
![]()
となり時間によらない.値はt=0のときのエネルギー値である.求めた解が正しいものであることが上の計算により確かめられた.最後に、もしmが大きければ上と同じ解をえるはずである.例えば、
![]()
![]()
![]()
![]()
より滑り落ちた距離xは
![]()
![]()
すなわち、
![]()
![]()
となり(物理的考察より符号を選んだ)同じであることがわかる.
![]()
![]()
![]()
![]()
![]()
![]()


以下は上に挿入したdynamic gifを作成したときの手順
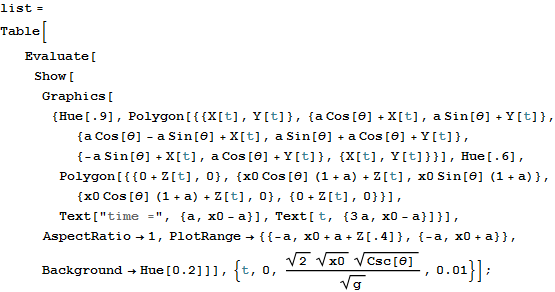
![]()
![]()