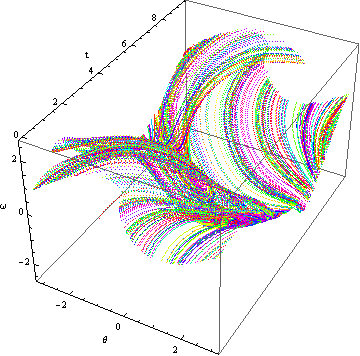
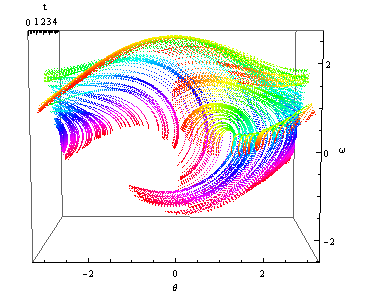
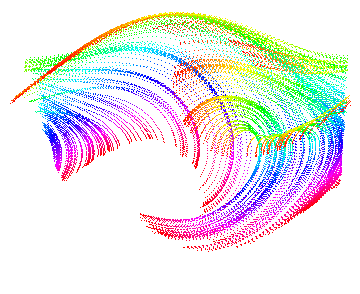
長さ L の糸の先に質量 m の振り子がぶら下がり、速度に比例する摩擦力 γ m L
、それに外力 
cos (
t) を受けていると考える．ここで γ は定数で減衰パラメターと呼ぶ．そのときのニュートン の運動方程式は、m L
θ + γ m L
+ W sinθ = 
cos (
t) とかける．W は重量、
は外力の角振動数である． ここで、系のパラメターの数を減らすために、振り子の自然振動数 
(= 
) が１であると仮定する．時間はしたがって無単位とみなす．この仮定のもとで、運動方程式は次のようにかきかえられる．ω’[t] + 1/q ω[t] + Sin[θ[t]] == g Cos[
t]ここで、q はクオリティーパラメター (quality parameter)、 g は外力振幅 (forcing amplitude)と呼ぶことにする． (g を重力の加速度と混同しないように．)
式をルンゲ・クッタ法を用いて数値的に解くことにする．まず、次の二つの関数を定義する．
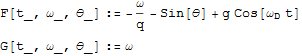
G[]がωだけのの関数であるのにわざわざ変数 t と θ まで加えたのは、ルンゲ・クッタ法をもっと一般の場合にも使えるようにという配慮と、また、変数の数をこのように増やしても、計算速度があまり変わらないということによる．
