2002.5.24 東洋大学 旭貴朗
Excelによる進化シミュレーション
1 はじめに
本稿では、遺伝的アルゴリズムによる最適化の方法を提示する。使用するソフトは、Microsoft社のExcel である。それを動かすための言語は、Visual Basic for Applicationである。
第2節では、遺伝子の進化をコンピュータで模擬する方法として、遺伝アルゴリズムについて解説する。第3節では、観測値に対して近似式を求めるという基本的な例題に対して、VBAプログラムを作成し、動かしてみる。変化の傾向や、必要なプログラミング知識について言及する。第4節では、遺伝アルゴリズムを、オプション取引における価格決定に適用する。最後の節は議論である。この方法の利点や欠点を考察する。
2 遺伝系
ここでは生物の進化、といっても人間以外の動物や植物、とくに昆虫レベルの生物を対象に議論を進める。
(1) 進化
ダーウィンの進化論では、種の進化を「突然変異と適者生存(自然選択)」というキーワードで説明している。環境が常に変化しているひとつの生物種の集団を考える。環境変化のため、その生物集団は常に生存の危機に遭遇している。しかし、生物集団には、まれに突然変異をもつ個体が生まれることがある。その個体が、たまたま他の個体よりもより良く環境に適しているならば、より多くの子孫を残すであろう。また環境に適応できない個体は死滅してゆくであろう。したがって、突然変異した環境適応度の高い個体の子孫が繁栄し、その生物種全体に占める割合を高くしてゆくだろう。これがダーウィンによる種の進化の説明方法である。
その後、優勢遺伝の法則やDNAの2重らせん構造の発見にともない、われわれが知っている生物学の教科書で習うような、「遺伝子の概念を中心とした近代的な説明方法」に改められた。ネオダーウィニズムである。遺伝子の突然変異だけでなく、「遺伝子交叉(交配)」によって両親の遺伝子が混合されることによる変化をも取り込むのである。
(2) 遺伝アルゴリズム
遺伝アルゴリズム (GA : Genetic Algorithm) は、コンピュータシミュレーションの中に、上記の3つの概念(遺伝子交叉、突然変異、適者生存)を実現し、進化をシミュレートしようというものである。具体的には、つぎのようなアルゴリズムとなっている。

図表 1 遺伝アルゴリズム
複数の個体から成る集団を考えよう。各個体の遺伝子は、コンピュータの中では記号列(数値を含む)で表現する。たとえば、2つの個体XとYの遺伝子を、それぞれ、x = x1x2x3x4x5、y = y1y2y3y4y5などと表わすのである。もしもこれらの個体が交配するならば、子供Zの遺伝子は、たとえば、z = x1x2x3y4y5となる。どこかで切れて、他方と結合するのである。これを遺伝子交叉という。まれに、突然変異が起こる時は、z´ = x1x2z3y4y5などとなる。
プログラム作成の観点からは、いくつかの約束がある。まず、遺伝子は、直列の記号列だけでなく、tree構造にするなど、いくらでも複雑に定義することが可能である。また、交叉の場所(切断点)は、モデル作成者が、あらかじめ決めておく。固定しても良いし、ランダムになるようにプログラムすることができる(random関数を使う)。突然変異の場所や時期、それに何に変異するのかは、もちろんランダムでなくてはならない。
さて、こうして生まれた次世代の子供たちは、自分たちが置かれている環境の中で生きてゆく。あるものはうまく生きてゆき、別のものは環境不適応のため、弱ってゆく。しかしここでは「生活すること」をシミュレーションすることはせず、環境適応度というものを考えてみる。
適応度とは、環境にどれくらい適応しているかを表す指標であり、数値で表現する。Zの適応度はf(Z)=0.8 、Z´の適応度はf(Z´)=0.7 といった具合に数値を割り当てる。ただし、関数fはすべての個体に適用するもので、すくなくとも同世代の中では一定のものを用いる。
子供の適応度が両親のものよりも低くなることもあるし、高くなることもある。たくさんの子供たちのなかで、適応度の高いものは生存確率も高く、繁殖力も高いだろう。したがって、適応度が高いものの間で交配させるようにペアを組む。適応度が低く、ペアにもれたものは死滅したものとみなされる。こうして新たな両親たちが、再び上の手順にしたがって、孫を生んでゆく。このような繰り返しが遺伝アルゴリズムである。
(3) 遺伝系の挙動
環境変化がある場合(関数fが変化した場合)、遺伝アルゴリズムを繰り返してゆくと、環境変化前の集団に広く分布していた遺伝子と、環境変化後の集団に広く分布する遺伝子は異なるのは当然である。一方、環境変化のない場合(関数fが一定の場合)では、世代が交代してゆくにつれて、もちろん適応度の高い遺伝子が集団に広がってゆく。
この「環境が一定のとき、その値を高くする遺伝子が増えてゆく」という傾向を利用すると、工学的な応用として、最適解計算が考えられる。上記の例では、与えられた5変数関数f(X) の最大値を達成するXを求めよ、という問題に相当する。適当な数値を何個か用意し、それら数値を遺伝子群とみなす。この遺伝子群に遺伝アルゴリズムを適用し、数万世代を経て生き残った数値(遺伝子)を見るのである。数学的にいえば、このやり方で生き残った数値は必ずしも最適解とはいえないが、なんらかの手がかりが得られる。
3 近似式の推定
ここでは表計算ソフトExcelのマクロ言語Visual Basic for Application (以下、VBAと略す)を利用し、簡単な問題に対して、遺伝アルゴリズムを用いたコンピュータ・シミュレーションを行なう。
(1) 例題:傾向の表現
たとえば、離散的な観測値があり、そこに比例の傾向があるとき、この傾向を直線で表現することができる。
| 年度x | 1 | 2 | 3 | 4 | 5 |
| 観測値 | 0.602 | 1.346 | 1.247 | 2.350 | 2.597 |
| 近似値 | 0.602 | 1.101 | 1.600 | 2.098 | 2.597 |
図表2 ある自治体の税収(単位:億円)
上記の表は、ある自治体における過去五年間の税収の記録である。税収は増加傾向にある。統計学では、この傾向を数式で表現することができる。最小2乗法を用いて、数式 y =0.103+ 0.499*x が得られ、x = 1,2,3,4,5 と代入すれば、だいたい一致することが分かる。これを近似式という。さらに、もしもx = 6 を代入すれば翌年の税収が予測できる。ただし、「このまま税収が伸びると仮定して」の話であるが。また、Excelの追加機能(アドイン)で、近似式を求めることもできる。
(2) 進化シミュレーション
しかし、ここでは統計学や追加機能を利用せず、遺伝アルゴリズムを用いたコンピュータ・シミュレーションで上記の近似式を作りたい。
まず、プログラミングにはいる前に、プログラミング方針を決めたい。決めるべきことは、何を遺伝子とし、何を適応度とするかである。求めたいのは近似式y = u1 + u2*xの係数u1、u2である。そこでまず、これらの係数を遺伝子とみなすことにする。たとえば個体の数を10とし、それぞれの名前をi =1,2,3,...,10と呼ぶことにすると、個体iの遺伝子はu1(i)とu2(i)である。この遺伝子にもとづく個体iによる税収の近似式をc(i,x) = u1(i) + u2(i)*xと書くことにする。
各個体のうち、どれがもっとも良い近似式を持っているのであろうか。与えられた観測値をc1(x)とすると、これとの差が小さくなるようにしたいので、各xに対する差の和を乖離度とする。乖離度 = Σ|c1(x) - c(i,x)|。すると乖離度が小さければ小さいほど、良い近似式であるということになる。逆にいえば、「マイナス乖離度」あるいは「1/乖離度」が適応度である。これが大きければ大きいほど、良い近似式である。しかし、ここでは、適応度に変換する手間をはぶき、乖離度のままプログラミングすることにする。以上により、遺伝子と適応度(乖離度)が決まった。
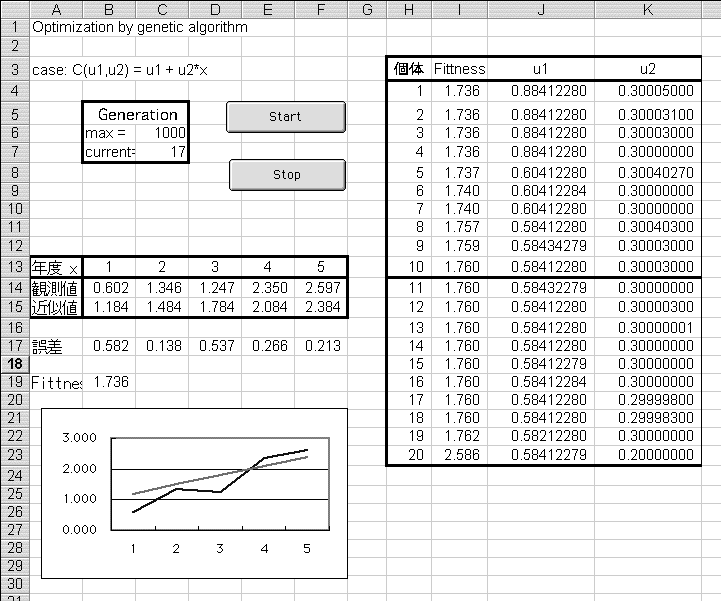
図表3 近似式の推定(Excel画面)
さて、上図はExcel画面である。左側には、観測値と近似値を比較するための表やグラフが表示されている。また観測値は、変更することができる。スタートボタンとストップボタンが配置されている。右側には、進化途中の各世代における全個体の遺伝子と適応度が表示される。
VBAプログラムは付録1を参照されたい。スタートボタンをクリックすると、このプログラムが動き出すのである。まず準備としてランダムに20個の遺伝子を発生させる(初期化)。つぎに、先頭から10個の個体を、この世代の親とし、残りの10個体は死滅したものとみなす(プログラム上は、単に無視するだけである)。
さて、10個体の親のうち、ふたつづつ5組のカップルを作り、遺伝子交配させて、子供をふたりづつ5組作成する。このとき、各子供の遺伝子は、両親の遺伝子(u1, u2)から半分づつもらうことにした。したがって、たとえば個体11と個体12は、個体1と個体2の子供である。
For i = 11 To 19 Step 2
u1(i) = u1(i - 10)
u2(i) = u2(i - 9)
u1(i + 1) = u1(i - 9)
u2(i + 1) = u2(i - 10)
Next i
突然変異は、各個体ごとに、ランダムに選んだ何らかの数値を加えたり減らしたりするようにした。たとえば、0.005を加算するか減算するかである。小数点以下何位まで0にするかは、ランダム関数を利用する。
その後、すべての個体について乖離度を計算し、良いものから順にソートする。計算結果は、表計算のシートに記入する。それが付録1のプログラムであり、図表1のアルゴリズムを実現している。各種コマンドの解説は、その知りたい単語を選択し、ヘルプ機能を使えばよい。
(3) 変化の傾向
スタートボタンをクリックしてこのプログラムを起動すると、進化のシミュレーションが開始される。このシステムの場合は、だいたい200世代くらいで、ほぼ大まかな推定が終わり、あとは微調整の段階にはいる。その様子は、グラフを見ていると分かる。近似値のグラフが、しだいに観測値に近付いてゆくのである。200世代を超えると、あとは子供の突然変異だけが繰り返され、親の個体1〜10は、ほとんど変化することはない。つまり定常状態にはいるのである。
4 オプション取引
オプション取引における契約に対する価格を決定する数式を、遺伝アルゴリズムを用いてもとめることを考える。
(1) 問題の所在
| | x1 | x2 | x3 | x4 | x5 |
| t1 | 0.500 | 1.000 | 1.500 | 2.150 | 2.500 |
| t2 | 1.000 | 1.875 | 2.250 | 2.950 | 3.375 |
| t3 | 1.875 | 2.500 | 2.875 | 3.250 | 3.875 |
| t4 | 2.500 | 3.000 | 3.500 | 4.375 | 4.625 |
| t5 | 3.875 | 4.375 | 4.875 | 5.500 | 5.875 |
図表4 板(オプション価格)
あるひとつのオプション商品があり、その契約のしかたが25種類用意されている。図表4は、それぞれの契約に対する実際の成約金額が記録されているものであり、市場では「板」と呼ばれている。契約のしかたは2次元に配置することができる。縦軸は「っっっp」、横軸は「@@@@@」を表している。成約金額をc1(t, x)と表すことにする。
ある統計的単純さを仮定すると、これらの値は、ある式cbs(t, x)によって求めることができると言われている。この式は、発見した2名の研究者にちなんで「ブラック=ショールズ式」と呼ばれている(彼らは、ノーベル経済学賞を獲得している)。式cbs(t, x)は、VBAであらわすと、
cbs = s * Application.NormSDist(d1) - Exp(-r * t) * s / x * Application.NormSDist(d2)
である。ただし、変数s、d1、r、d2は、前提から計算される数値が代入される。また、関数NormSDist()は、正規分布をあらわす。しかし、本稿の範囲では、変数の意味や関数の意味については考える必要はない。単に、与えられているものとする。
(2) 求解のためのプログラミング
しかし、ブラック=ショールズ式cbs(t, x)は統計的単純さを前提としているので、現実の「板」の数値c1(t, x)にぴったり一致するわけではない。実際にはわずかにずれるのである。そこで、いちおうcbs(t, x)を利用するものの、より現実に適合する式に変型してみたい。それが、ここでの問題意識である。具体的には、仮に新しい式を、c(i, t, x) = u1* cbs(t, x) + u2*xとして、現実に適合する係数u1、u2を求めるという問題を考えてみたい。
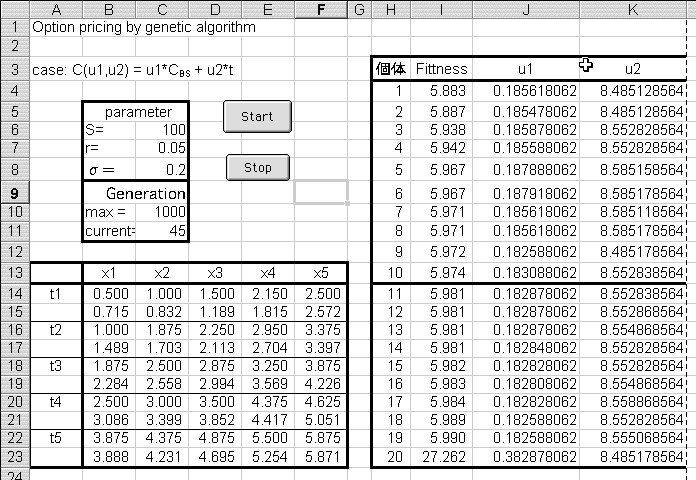
図表5 オプション取引の価格に対する近似
これは2つの係数をもつ式が観測値を近似する問題であり、前節で考えた近似式を求める問題と似ている。実際、似たような画面設計を行ない(上図)、似たようなVBAコードを作成する。やはり、係数u1、u2を遺伝子にもつ個体の集団を考えて、進化のシミュレーションを行なうことになる。適応度は、 f(i, x,t) = Σ|cbs(t, x) - c(i, t, x)|である。どんなコードになるかは読者の想像にまかせる。
5 おわりに
遺伝的アルゴリズムにもとづき、確かに簡単にプログラムが作成できる。また、進化をシミュレートすることによって、最適化を行なうこともできる。利点は、適応度関数を自由に設定できることである。
しかし、遺伝的アルゴリズムは、万能ではない。欠点として、シミュレーションで得られた結果が、局所的に最適であることは確かであるが、必ずしも全体最適解になるとは限らないことである。
また、案として検討する数式は、アドホックなものであることである。たとえば、前節では1次式u1* cbs(t, x) + u2*xを検討対象にしたが、2次式でも可能である。1次式にしたのに、数学的な確固たる理由はない。
しかしながら、それでも役に立てばよいという工学的な立場をとるならば、話は別である。特定の許容範囲を設定し、この範囲内に近似が成り立つならばいいのだという利用のしかたもある。この場合は、それぞれのデータに対して、許容される近似式を、遺伝的計算によって求め、そのつど現実の意思決定の支援に役立てるという手順が想定される。これは方法論の問題である。
付録1 遺伝アルゴリズムによる、近似式の推定プログラム
Global flag As Boolean
Private Sub ボタン4_Click()
'初期化(変数宣言)
Randomize
Dim c(11 To 20, 1 To 5), c1(1 To 5), ar(1 To 20) As Double
flag = False
'初期個体を発生
Dim u1(1 To 20), u2(1 To 20) As Double
For i = 1 To 20
u1(i) = Rnd() * 10
u2(i) = Rnd() * 10
ar(i) = 200
Next i
'メイン処理
For generation = 1 To Cells(6, 3).Value
'世代数を記入
Cells(7, 3).Value = generation
'生存個体を決定
'次世代の親は先頭から10個までを利用する
'遺伝子交叉を行なう
For i = 11 To 19 Step 2
u1(i) = u1(i - 10)
u2(i) = u2(i - 9)
u1(i + 1) = u1(i - 9)
u2(i + 1) = u2(i - 10)
Next i
'突然変異を行なう
For i = 11 To 20
u1(i) = u1(i) + randomNum()
u2(i) = u2(i) + randomNum()
If u1(i) < 0 Then u1(i) = 0
If u2(i) < 0 Then u2(i) = 0
Next i
'適応度を計算
For i = 11 To 20
ar(i) = 0
Next i
For i = 11 To 20
For x = 1 To 5
c(i, x) = u1(i) + u2(i) * x
c1(x) = Cells(14, x + 1).Value
ar(i) = Abs(c(i, x) - c1(x)) + ar(i)
Next x
Next i
'適応度の高いもの順にソート
For i = 1 To 19
For j = i + 1 To 20
If ar(i) > ar(j) Then
tmp = ar(i)
tmpu1 = u1(i)
tmpu2 = u2(i)
ar(i) = ar(j)
u1(i) = u1(j)
u2(i) = u2(j)
ar(j) = tmp
u1(j) = tmpu1
u2(j) = tmpu2
End If
Next j
Next i
'個体の属性を記入
For i = 1 To 20
Cells(3 + i, 9).Value = ar(i)
Cells(3 + i, 10) = u1(i)
Cells(3 + i, 11) = u2(i)
Next i
'最適個体の表現型特性値を記入
If (generation Mod 3) = 0 Then
For x = 1 To 5
Cells(15, x + 1).Value = u1(1) + u2(1) * x
Next x
End If
'ストップボタンの検出
DoEvents
If flag = True Then Exit For
Next generation
For x = 1 To 5
Cells(15, x + 1).Value = u1(1) + u2(1) * x
Next x
End Sub
Sub ボタン12_Click()
'ストップボタン
flag = True
End Sub
Function randomNum()
If Rnd() > 0.5 Then
signal = 1
Else
signal = -1
End If
ww = 6
rr = Rnd() * 100
If rr < 2 Then ww = 6
If 2 <= rr Then ww = 5
If 10 <= rr Then ww = 4
If 20 <= rr Then ww = 3
If 40 <= rr Then ww = 2
If 70 <= rr Then ww = 1
w1 = Int(Rnd() * 10)
randomNum = signal * ww * 0.1 ^ w1
End Function
参考文献
1)John H. Holland (著)『遺伝アルゴリズムの理論―自然・人工システムにおける適応 』森北出版 (1999/05/01)



